
| AЃЎ | [-15ЃЌ25ЃЉ | BЃЎ | [-15ЃЌ15] | CЃЎ | [0ЃЌ25ЃЉ | DЃЎ | [0ЃЌ15] |
ЗжЮі ИљОн$|{\overrightarrow{OA}+\overrightarrow{OB}}|Ён\frac{1}{2}|{\overrightarrow{AB}}|$=$\frac{1}{2}$|$\overrightarrow{OB}$-$\overrightarrow{OA}$|ЃЌСНБпЦНЗНЧѓГі$\overrightarrow{OA}$•$\overrightarrow{OB}$Ён-15ЃЛ
РћгУЦНУцЯђСПЪ§СПЛ§ЕФЖЈвхЧѓГі$\overrightarrow{OA}$•$\overrightarrow{OB}$ЃМ25ЃЌДгЖјЕУГі$\overrightarrow{OA}•\overrightarrow{OB}$ЕФШЁжЕЗЖЮЇЃЎ
НтД№ НтЃКдкЕШбќЁїAOBжаЃЌ|OA|=|OB|=5ЃЌ
$|{\overrightarrow{OA}+\overrightarrow{OB}}|Ён\frac{1}{2}|{\overrightarrow{AB}}|$=$\frac{1}{2}$|$\overrightarrow{OB}$-$\overrightarrow{OA}$|ЃЌ
Ёр${ЃЈ\overrightarrow{OA}+\overrightarrow{OB}ЃЉ}^{2}$Ён$\frac{1}{4}$${ЃЈ\overrightarrow{OB}-\overrightarrow{OA}ЃЉ}^{2}$ЃЌ
МД${\overrightarrow{OA}}^{2}$+2$\overrightarrow{OA}$•$\overrightarrow{OB}$+${\overrightarrow{OB}}^{2}$Ён$\frac{1}{4}$${\overrightarrow{OB}}^{2}$-$\frac{1}{2}$$\overrightarrow{OA}$•$\overrightarrow{OB}$+$\frac{1}{4}$${\overrightarrow{OA}}^{2}$ЃЌ
Ёр25+2$\overrightarrow{OA}$•$\overrightarrow{OB}$+25Ён$\frac{25}{4}$-$\frac{1}{2}$$\overrightarrow{OA}$•$\overrightarrow{OB}$+$\frac{25}{4}$ЃЌ
НтЕУ$\overrightarrow{OA}$•$\overrightarrow{OB}$Ён-15ЃЛ
гж$\overrightarrow{OA}$•$\overrightarrow{OB}$=5ЁС5ЁСcosЁЯAOBЃМ25ЃЌ
Ёр-15Ём$\overrightarrow{OA}$•$\overrightarrow{OB}$ЃМ25ЃЛ
МД$\overrightarrow{OA}•\overrightarrow{OB}$ЕФШЁжЕЗЖЮЇЪЧ[-15ЃЌ25ЃЉЃЎ
ЙЪбЁЃКAЃЎ
ЕуЦР БОЬтПМВщСЫЦНУцЯђСПЪ§СПЛ§ЕФдЫЫуЮЪЬтЃЌЪЧзлКЯЬтЃЎ


 УППЮБиСЗЯЕСаД№АИ
УППЮБиСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{4}{3}$ | BЃЎ | $\frac{\sqrt{5}}{3}$ | CЃЎ | $\frac{2}{3}$ | DЃЎ | $\frac{\sqrt{3}}{3}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
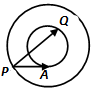 ШчЭМЭЌаФдВжаЃЌДѓЁЂаЁдВЕФАыОЖЗжБ№ЮЊ2КЭ1ЃЌЕуPдкДѓдВЩЯЃЌPAгыаЁдВЯрЧагкЕуAЃЌQЮЊаЁдВЩЯЕФЕуЃЌдђ$\overrightarrow{PA}•\overrightarrow{PQ}$ЕФШЁжЕЗЖЮЇЪЧ[3-$\sqrt{3}$ЃЌ3+$\sqrt{3}$]ЃЎ
ШчЭМЭЌаФдВжаЃЌДѓЁЂаЁдВЕФАыОЖЗжБ№ЮЊ2КЭ1ЃЌЕуPдкДѓдВЩЯЃЌPAгыаЁдВЯрЧагкЕуAЃЌQЮЊаЁдВЩЯЕФЕуЃЌдђ$\overrightarrow{PA}•\overrightarrow{PQ}$ЕФШЁжЕЗЖЮЇЪЧ[3-$\sqrt{3}$ЃЌ3+$\sqrt{3}$]ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 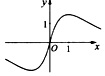 | BЃЎ | 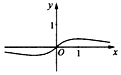 | CЃЎ | 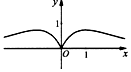 | DЃЎ | 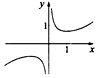 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
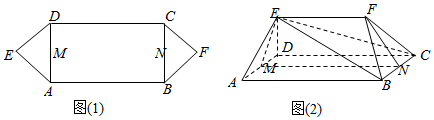
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com