
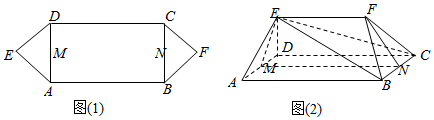
分析 (1)由题意,点E在底面ABCD的射影在MN上,可设为点P,同理,点F在底面ABCD的射影在MN上,可设为点Q,推导出平面EMP⊥平面ABCD,平面FNQ⊥平面ABCD,由结论2能证明E、F、M、N四点共面.
(2)三棱锥E-BCF的体积VE-BCF=VABCDEF-VE-ABCD,由此能求出结果.
解答 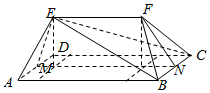 证明:(1)由题意,点E在底面ABCD的射影在MN上,可设为点P,
证明:(1)由题意,点E在底面ABCD的射影在MN上,可设为点P,
同理,点F在底面ABCD的射影在MN上,可设为点Q,
则EP⊥平面ABCD,FQ⊥平面ABCD,
∴平面EMP⊥平面ABCD,平面FNQ⊥平面ABCD,
又MN?平面ABCD,MN?平面EMP,MN?平面FNQ,
由结论2:过平面内一条直线作该平面的垂面,有且只有一个,
得到E、F、M、N四点共面.
解:(2)∵二面角E-AD-B和二面角F-BC-A都是60°,
∴∠EMP=∠FNQ=60°,∴EP=EM•sin60°=$\frac{\sqrt{3}}{2}$,
∴三棱锥E-BCF的体积:
VE-BCF=VABCDEF-VE-ABCD
=2×$\frac{1}{3}×(\frac{1}{2}×2)×\frac{\sqrt{3}}{2}$+($\frac{1}{2}×\frac{\sqrt{3}}{2}×2$)×3-$\frac{1}{3}×(4×2)$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查四点共面的证明,考查三棱锥的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合思想、化归与转化思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-15,25) | B. | [-15,15] | C. | [0,25) | D. | [0,15] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
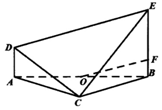 如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.
如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 社区服务是综合实践活动课程的重要内容.上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[65,70),[70,75),[75,80),[80,85),[85,90)(单位:小时)进行统计,其频率分布直方图如图所示.
社区服务是综合实践活动课程的重要内容.上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[65,70),[70,75),[75,80),[80,85),[85,90)(单位:小时)进行统计,其频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,-2) | B. | (2,2) | C. | (-2,-2) | D. | (-2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m∥γ,α⊥γ | B. | n∥β,α⊥γ | C. | β∥γ,α⊥γ | D. | m⊥n,α⊥γ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{121}{2}$,81] | B. | [$\frac{121}{2}$,73] | C. | [65,73] | D. | [65,81] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com