
【题目】国际羽毛球比赛规则从2006年5月开始,正式决定实行21分的比赛规则和每球得分制,并且每次得分者发球,所有单项的每局获胜分至少是21分,最高不超过30分,即先到21分的获胜一方赢得该局比赛,如果双方比分为![]() 时,获胜的一方需超过对方2分才算取胜,直至双方比分打成
时,获胜的一方需超过对方2分才算取胜,直至双方比分打成![]() 时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为
时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为![]() ,甲接发球贏球的概率为
,甲接发球贏球的概率为![]() ,则在比分为
,则在比分为![]() ,且甲发球的情况下,甲以
,且甲发球的情况下,甲以![]() 赢下比赛的概率为( )
赢下比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款,法国8款、荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国,![]() 地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区一婴幼儿用品商店在售某品牌的奶粉共6袋,这6袋奶粉中有4袋含有芳香矿物油成分,则随机抽取3袋恰有2袋含有芳香经矿物油成分的概率为( )
地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区一婴幼儿用品商店在售某品牌的奶粉共6袋,这6袋奶粉中有4袋含有芳香矿物油成分,则随机抽取3袋恰有2袋含有芳香经矿物油成分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且此抛物线的准线被椭圆C截得的弦长为1.
的焦点重合,且此抛物线的准线被椭圆C截得的弦长为1.
(I)求椭圆C的标准方程;
(II)直线l交椭圆C于A,B两点,线段AB的中点为![]() ,直线m是线段AB的垂直平分线,试问直线
,直线m是线段AB的垂直平分线,试问直线![]() 过定点坐标.
过定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() ,直线
,直线![]() 与y轴交于点P.且与椭圆交于A,B两点.A为椭圆的右顶点,B在x轴上的射影恰为
与y轴交于点P.且与椭圆交于A,B两点.A为椭圆的右顶点,B在x轴上的射影恰为![]() 。
。
(1)求椭圆E的方程;
(2)M为椭圆E在第一象限部分上一点,直线MP与椭圆交于另一点N,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 满足
满足![]() 且
且![]() 是它的零点,则函数
是它的零点,则函数![]() 是“有趣的”,例如
是“有趣的”,例如![]() 就是“有趣的”,已知
就是“有趣的”,已知![]() 是“有趣的”.
是“有趣的”.
(1)求出b、c并求出函数![]() 的单调区间;
的单调区间;
(2)若对于任意正数x,都有![]() 恒成立,求参数k的取值范围.
恒成立,求参数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
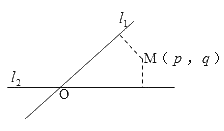
【题目】如图,平面内两条直线![]() 和
和![]() 相交于点
相交于点![]() ,构成的四个角中的锐角为
,构成的四个角中的锐角为![]() .对于平面上任意一点
.对于平面上任意一点![]() ,若
,若![]() ,
,![]() 分别是
分别是![]() 到直线
到直线![]() 和
和![]() 的距离,则称有序非负实数对
的距离,则称有序非负实数对![]() 是点
是点![]() 的“距离坐标”,给出下列四个命题:
的“距离坐标”,给出下列四个命题:
①![]() 点有且仅有两个;
点有且仅有两个;
②![]() 点有且仅有4个;
点有且仅有4个;
③若![]() ,则点
,则点![]() 的轨迹是两条过
的轨迹是两条过![]() 点的直线;
点的直线;
④满足![]() 的所有点
的所有点![]() 位于一个圆周上.
位于一个圆周上.
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
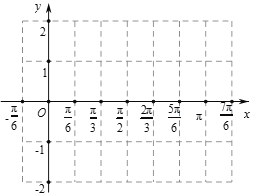
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经统计,用于数学学习的时间(单位:小时)与成绩(单位:分)近似于线性相关关系.对某小组学生每周用于数学的学习时间![]() 与数学成绩
与数学成绩![]() 进行数据收集如下:
进行数据收集如下:

由样本中样本数据求得回归直线方程为![]() ,则点
,则点![]() 与直线
与直线![]() 的位置关系是( )
的位置关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]() 与
与![]() 的大小无法确定
的大小无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 在[0,7]上有1和6两个零点,且函数
在[0,7]上有1和6两个零点,且函数![]() 与函数
与函数![]() 都是偶函数,则
都是偶函数,则![]() 在[0,2019]上的零点至少有( )个
在[0,2019]上的零点至少有( )个
A.404B.406C.808D.812
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com