
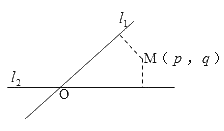
【题目】如图,平面内两条直线![]() 和
和![]() 相交于点
相交于点![]() ,构成的四个角中的锐角为
,构成的四个角中的锐角为![]() .对于平面上任意一点
.对于平面上任意一点![]() ,若
,若![]() ,
,![]() 分别是
分别是![]() 到直线
到直线![]() 和
和![]() 的距离,则称有序非负实数对
的距离,则称有序非负实数对![]() 是点
是点![]() 的“距离坐标”,给出下列四个命题:
的“距离坐标”,给出下列四个命题:
①![]() 点有且仅有两个;
点有且仅有两个;
②![]() 点有且仅有4个;
点有且仅有4个;
③若![]() ,则点
,则点![]() 的轨迹是两条过
的轨迹是两条过![]() 点的直线;
点的直线;
④满足![]() 的所有点
的所有点![]() 位于一个圆周上.
位于一个圆周上.
其中正确命题的个数是( )
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在极坐标系(与平面直角坐标系
为参数).在极坐标系(与平面直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上的任意一点,求点
上的任意一点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际羽毛球比赛规则从2006年5月开始,正式决定实行21分的比赛规则和每球得分制,并且每次得分者发球,所有单项的每局获胜分至少是21分,最高不超过30分,即先到21分的获胜一方赢得该局比赛,如果双方比分为![]() 时,获胜的一方需超过对方2分才算取胜,直至双方比分打成
时,获胜的一方需超过对方2分才算取胜,直至双方比分打成![]() 时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为
时,那么先到第30分的一方获胜.在一局比赛中,甲发球赢球的概率为![]() ,甲接发球贏球的概率为
,甲接发球贏球的概率为![]() ,则在比分为
,则在比分为![]() ,且甲发球的情况下,甲以
,且甲发球的情况下,甲以![]() 赢下比赛的概率为( )
赢下比赛的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正整数集合![]() ,如果任意去掉其中一个元素
,如果任意去掉其中一个元素![]() 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合![]() 为“可分集合”.
为“可分集合”.
(1)判断集合![]() 和
和![]() 是否是“可分集合”(不必写过程);
是否是“可分集合”(不必写过程);
(2)求证:五个元素的集合![]() 一定不是“可分集合”;
一定不是“可分集合”;
(3)若集合![]() 是“可分集合”.
是“可分集合”.
①证明:![]() 为奇数;
为奇数;
②求集合![]() 中元素个数的最小值.
中元素个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴极坐标,曲线
轴非负半轴为极轴极坐标,曲线![]() 的方程:
的方程: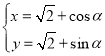 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程:
的方程: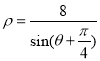 .
.
(1)求曲线![]() 和曲线
和曲线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)从![]() 上任意一点
上任意一点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求切线长
,求切线长![]() 的最小值及此时点
的最小值及此时点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() .
.
(1)若![]() ,试断
,试断![]() 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)若![]() 证明
证明![]() 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式;
的通项公式;
(3)对(2)中的数列![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立,若存在,求出数列
都成立,若存在,求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com