
【题目】如图,已知扇形的圆心角∠AOB=![]() ,半径为
,半径为![]() ,若点C是
,若点C是![]() 上的一动点(不与点A,B重合).
上的一动点(不与点A,B重合).

(1)若弦![]() ,求
,求![]() 的长;
的长;
(2)求四边形OACB面积的最大值.
科目:高中数学 来源: 题型:
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(Ⅲ)求![]() 关于
关于![]() 的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过
的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过![]() 万元.
万元.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
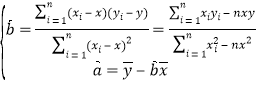
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 为圆周上一点,
为圆周上一点,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,且使得
,且使得![]() 平面
平面![]() ?若存在,求出点
?若存在,求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下几个命题中:
①线性回归直线方程![]() 恒过样本中心
恒过样本中心![]() ;
;
②用相关指数![]() 可以刻画回归的效果,值越小说明模型的拟合效果越好;
可以刻画回归的效果,值越小说明模型的拟合效果越好;
③随机误差是引起预报值![]() 和真实值
和真实值![]() 之间存在误差的原因之一,其大小取决于随机误差的方差;
之间存在误差的原因之一,其大小取决于随机误差的方差;
④在含有一个解释变量的线性模型中,相关指数![]() 等于相关系数
等于相关系数![]() 的平方.
的平方.
其中真命题的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
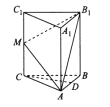
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上运动.
上运动.
(1)当![]() 是棱
是棱![]() 的中点时,求证:
的中点时,求证: ![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成的角的正切值为
所成的角的正切值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年5月21日5点28分,在我国西昌卫星发射中心,由中国航天科技集团有限公司抓总研制的嫦娥四号中继星“鹊桥”搭乘长征四号丙运载火箭升空,这标志着我国在月球探测领域取得新的突破.早在1671年,两位法国天文学家就已经成功测量出了地球与月球之间的距离,接下来,让我们重走这两位科学家的测量过程.如图,设O为地球球心,C为月球表面上一点,A,B为地球上位于同一子午线(经线)上的两点,地球半径记为R.

步骤一:经测量,A,B两点的纬度分别为北纬![]() 和南纬
和南纬![]() ,即
,即![]() ,可求得
,可求得![]() ;
;
步骤二:经测量计算,![]() ,
,![]() ,计算
,计算![]() ;
;
步骤三:利用以上测量及计算结果,计算![]() .
.
请你用解三角形的相关知识,求出步骤二三中的![]() 及
及![]() 的值(结果均用
的值(结果均用![]() ,
,![]() ,R表示).
,R表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2-2x+1.
(1)试讨论函数f(x)的单调性;
(2)若![]() ≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
(3)在(2)的条件下,求证:g(a)≥![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com