【题目】2018年5月21日5点28分，在我国西昌卫星发射中心，由中国航天科技集团有限公司抓总研制的嫦娥四号中继星“鹊桥”搭乘长征四号丙运载火箭升空，这标志着我国在月球探测领域取得新的突破.早在1671年，两位法国天文学家就已经成功测量出了地球与月球之间的距离，接下来，让我们重走这两位科学家的测量过程.如图，设O为地球球心，C为月球表面上一点，A，B为地球上位于同一子午线(经线)上的两点，地球半径记为R.
步骤一:经测量，A，B两点的纬度分别为北纬
和南纬
，即
，可求得
;
步骤二:经测量计算，
，
，计算
;
步骤三:利用以上测量及计算结果，计算
.
请你用解三角形的相关知识，求出步骤二三中的及的值(结果均用
，
，R表示).
七彩题卡口算应用一点通系列答案科目：高中数学 来源： 题型：
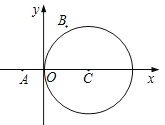
【题目】如图，在平面直角坐标系
中，已知圆
及点
，
．
（1）若直线
平行于
，与圆
相交于
，
两点，
，求直线
的方程；
（2）在圆
上是否存在点
，使得
？若存在，求点的个数；若不存在，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】科研人员在对某物质的繁殖情况进行调查时发现，1月、2月、3月该物质的数量分别为3、5、9个单位.为了预测以后各月该物质的数量，甲选择了模型
，乙选择了模型
，其中y为该物质的数量，x为月份数，a，b，c，p，q，r为常数.
（1）若5月份检测到该物质有32个单位，你认为哪个模型较好，请说明理由.
（2）对于乙选择的模型，试分别计算4月、7月和10月该物质的当月增长量，从计算结果中你对增长速度的体会是什么？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线
： 
与椭圆
有且只有一个公共点．
（Ⅰ）求椭圆
的方程及点
的坐标；
（Ⅱ）设
是坐标原点，直线
平行于
，与椭圆
交于不同的两点
、
，且与直线
交于点
，证明：存在常数
，使得
，并求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
（
，且
）.
（1）当
（其中
，且t为常数）时，
是否存在最小值，如果存在，求出最小值；如果不存在，请说明理由；
（2）当
时，求满足不等式
的实数x的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区为了解群众上下班共享单车使用情况，根据年龄按分层抽样的方式调查了该地区50名群众，他们的年龄频数及使用共享单车人数分布如下表：
年龄段 | 20~29 | 30~39 | 40~49 | 50~60 |
频数 | 12 | 18 | 15 | 5 |
经常使用共享单车 | 6 | 12 | 5 | 1 |
（1）由以上统计数据完成下面的
列联表，并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异？
年龄低于40岁 | 年龄不低于40岁 | 总计 | |
经常使用共享单车 | |||
不经常使用共享单车 | |||
总计 |
附：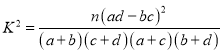
，
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
（2）若采用分层抽样的方式从年龄低于40岁且经常使用共享单车的群众中选出6人，再从这6人中随机抽取2人，求这2人中恰好有1人年龄在30~39岁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
