
【题目】已知函数f(x)=ax2-2x+1.
(1)试讨论函数f(x)的单调性;
(2)若![]() ≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
≤a≤1,且f(x)在[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a),求g(a)的表达式;
(3)在(2)的条件下,求证:g(a)≥![]() .
.
【答案】(1)见解析.(2)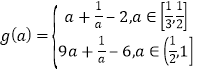 ;(3)详见解析.
;(3)详见解析.
【解析】
(1)分成![]() 三类,讨论函数的单调区间.(2)对函数进行配方,根据对称轴的位置对参数
三类,讨论函数的单调区间.(2)对函数进行配方,根据对称轴的位置对参数![]() 进行分类讨论,由此求得最大值和最小值,也即
进行分类讨论,由此求得最大值和最小值,也即![]() 的表达式.(3)利用导数求得
的表达式.(3)利用导数求得![]() 的单调区间,由此求得
的单调区间,由此求得![]() 的最小值,以此证明不等式成立.
的最小值,以此证明不等式成立.
(1)当a=0时,函数f(x)=-2x+1在(-∞,+∞)上为减函数;
当a>0时,抛物线f(x)=ax2-2x+1开口向上,对称轴为x=![]() ,
,
故函数f(x)在![]() 上为减函数,在
上为减函数,在![]() 上为增函数;
上为增函数;
当a<0时,抛物线f(x)=ax2-2x+1开口向下,对称轴为x=![]() ,
,
故函数f(x)在![]() 上为增函数,在
上为增函数,在![]() 上为减函数.
上为减函数.
(2)∵f(x)=a![]() 2+1-
2+1-![]() ,
,
由![]() ≤a≤1得1≤
≤a≤1得1≤![]() ≤3,∴N(a)=f
≤3,∴N(a)=f![]() =1-
=1-![]() .
.
当1≤![]() <2,即
<2,即![]() <a≤1时,M(a)=f(3)=9a-5,
<a≤1时,M(a)=f(3)=9a-5,
故g(a)=9a+![]() -6;
-6;
当2≤![]() ≤3,即
≤3,即![]() ≤a≤
≤a≤![]() 时,M(a)=f(1)=a-1,
时,M(a)=f(1)=a-1,
故g(a)=a+![]() -2.
-2.
∴g(a)=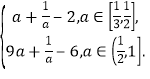
(3)证明:当a∈![]() 时,g′(a)=1-
时,g′(a)=1-![]() <0,
<0,
∴函数g(a)在![]() 上为减函数;
上为减函数;
当a∈![]() 时,g′(a)=9-
时,g′(a)=9-![]() >0,
>0,
∴函数g(a)在![]() 上为增函数,
上为增函数,
∴当a=![]() 时,g(a)取最小值,g(a)min=
时,g(a)取最小值,g(a)min=![]() =
=![]() .
.
故g(a)≥![]() .
.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ,且
,且![]() ).
).
(1)当![]() (其中
(其中![]() ,且t为常数)时,
,且t为常数)时,![]() 是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由;
是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由;
(2)当![]() 时,求满足不等式
时,求满足不等式![]() 的实数x的取值范围.
的实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图象在
的图象在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若函数![]() 存在单调递减区间,求实数
存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() (
(![]() )是函数
)是函数![]() 的两个极值点,若
的两个极值点,若![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年国际数学家大会在北京召开,会标是以我国古代数学家赵爽的弦图为基础设计.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图)如果小正方形的边长为1,大正方形的边长为5,直角三角形中较小的锐角为![]() ,则
,则![]() ( )
( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在极坐标系中,圆C的极坐标方程为:
为参数),在极坐标系中,圆C的极坐标方程为:![]()
(1)求圆C的直角坐标方程;
(2)设圆C与直线![]() 交于
交于![]() 两点,若点的坐标为
两点,若点的坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区为了解群众上下班共享单车使用情况,根据年龄按分层抽样的方式调查了该地区50名群众,他们的年龄频数及使用共享单车人数分布如下表:
年龄段 | 20~29 | 30~39 | 40~49 | 50~60 |
频数 | 12 | 18 | 15 | 5 |
经常使用共享单车 | 6 | 12 | 5 | 1 |
(1)由以上统计数据完成下面的![]() 列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?
列联表,并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异?
年龄低于40岁 | 年龄不低于40岁 | 总计 | |
经常使用共享单车 | |||
不经常使用共享单车 | |||
总计 |
附: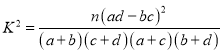 ,
,![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
(2)若采用分层抽样的方式从年龄低于40岁且经常使用共享单车的群众中选出6人,再从这6人中随机抽取2人,求这2人中恰好有1人年龄在30~39岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为x、y,设O为坐标原点,点P的坐标为![]() 记
记![]() .
.
(1)求随机变量![]() 的最大值,并求事件“
的最大值,并求事件“![]() 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com