分析:(1)在平面BC1D内找到一条直线与已知直线AB1平行,根据线面平行的判定定理证明线面平行,而找平行的方法一般是找三角形的中位线或找平行四边形.
(2)根据题中的垂直关系表达出四棱锥的体积进而得到等式求出BC的数值,结合这题中的线面垂直关系作出二面角,再证明此角就是所求角然后求出即可.
解答:解:

(1)证明:连接B
1C,设B
1C与BC
1相交于点O,连接OD,
∵四边形BCC
1B
1是平行四边形,
∴点O为B
1C的中点.
∵D为AC的中点,
∴OD为△AB
1C的中位线,
∴OD∥AB
1.
∵OD?平面BC
1D,AB
1?平面BC
1D,
∴AB
1∥平面BC
1D.
(2)解:依题意知,AB=BB
1=2,
∵AA
1⊥平面ABC,AA
1?平面AA
1C
1C,
∴平面ABC⊥平面AA
1C
1C,且平面ABC∩平面AA
1C
1C=AC.
作BE⊥AC,垂足为E,则BE⊥平面AA
1C
1C,
设BC=a,
在Rt△ABC中,
AC==,
BE==,
∴四棱锥B-AA
1C
1D的体积
V=×(A1C1+AD)•AA1•BE=
××2×=a.
依题意得,a=3,即BC=3.
∵AB⊥BC,AB⊥BB
1,BC∩BB
1=B,BC?平面BB
1C
1C,BB
1?平面BB
1C
1C,
∴AB⊥平面BB
1C
1C.
取BC的中点F,连接DF,则DF∥AB,且
DF=AB=1.
∴DF⊥平面BB
1C
1C.
作FG⊥BC
1,垂足为G,连接DG,
由于DF⊥BC
1,且DF∩FG=F,
∴BC
1⊥平面DFG.
∵DG?平面DFG,
∴BC
1⊥DG.
∴∠DGF为二面角C-BC
1-D的平面角.
由Rt△BGF~Rt△BCC
1,得
=,
得
GF===,
在Rt△DFG中,
tan∠DGF==
.
∴二面角C-BC
1-D的正切值为
.
点评:解决此类问题的关键是熟悉几何体的结构便于利用题中的线面、线线关系解决空间角、空间距离与几何体的体积等问题.

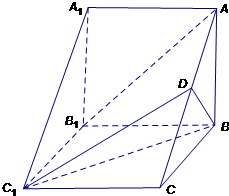 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,A1A=AB=2.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,A1A=AB=2. (1)证明:连接B1C,设B1C与BC1相交于点O,连接OD,
(1)证明:连接B1C,设B1C与BC1相交于点O,连接OD,

 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( ) 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.