
已知函数f(x)=x2+2ax+1(a∈R),f′(x)是f(x)的导函数.
(1)若x∈[-2,-1],不等式f(x)≤f′(x)恒成立,求a的取值范围;
(2)解关于x的方程f(x)=|f′(x)|;
(3)设函数g(x)=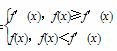 ,求g(x)在x∈[2,4]时的最小值.
,求g(x)在x∈[2,4]时的最小值.
解 (1)因为f(x)≤f′(x),所以x2-2x+1≤2a(1-x),
又因为-2≤x≤-1,
所以a≥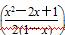 max在x∈[-2,-1]时恒成立,因为
max在x∈[-2,-1]时恒成立,因为 ≤
≤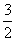 ,
,
所以a≥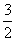 .
. (4分)
(4分)
(2)因为f(x)=|f′(x)|,所以x2+2ax+1=2|x+a|,
所以(x+a)2-2|x+a|+1-a2=0,则|x+a|=1+a或|x+a|=1-a.(7分)
①当a<-1时,|x+a|=1-a,所以x=-1或x=1-2a;
②当-1≤a≤1时,|x+a|=1-a或|x+a|=1+a,
所以x=±1或x=1-2a或x =-(1+2a);
=-(1+2a);
③当a>1时,|x+a|=1+a,所以x=1或x=-(1+2a).(10分)
(3)因为f(x)-f′(x)=(x-1)[x-(1-2a)],g(x)=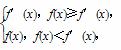
①若a≥-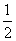 ,则x∈[2,4]时,f(x)≥f′(x),所以g(x)=f′(x)=2x+2a,
,则x∈[2,4]时,f(x)≥f′(x),所以g(x)=f′(x)=2x+2a,
从而g(x)的最小值为g(2)=2a+4;( 12分)
12分)
②若 a<-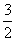 ,则x∈[2,4]时,f(x)<f′(x),所以g(x)=f(x)=x2+2ax+1,
,则x∈[2,4]时,f(x)<f′(x),所以g(x)=f(x)=x2+2ax+1,
当-2≤a<-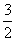 时,g(x)的最小值为g(2)=4a+5,
时,g(x)的最小值为g(2)=4a+5,
当-4<a<-2时,g(x)的最小值为g(-a)=1-a2,
当a≤-4时,g(x)的最小值为g(4)=8a+17.(14分)
③若-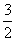 ≤a<-
≤a<-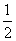 ,则x∈[2,4]时,
,则x∈[2,4]时,
g(x)=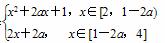
当x∈[2,1-2a)时,g(x)最小值为g(2)=4a+5;
当x∈[1-2a,4]时,g(x)最小值为g(1-2a)=2-2a.
因为-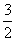 ≤a<-
≤a<-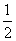 ,(4a+5)-(2-2a)=6a+3<0,
,(4a+5)-(2-2a)=6a+3<0,
所以g(x)最小值为4a+5,
 综上所述,
综上所述,
[g(x)]min=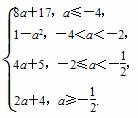


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
如图,从参加环保知识竞赛的学生中抽出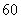 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
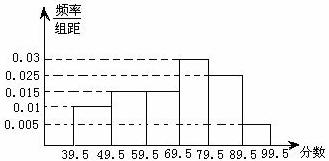
(1) 这一组的频数、频率分别是
这一组的频数、频率分别是
(2)估计这次环保知识竞赛的及格率(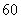 分及以上为及格)
分及以上为及格)
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{bn}满足bn+2=-bn+1-bn(n∈N*),b2=2b1.
(1)若b3=3,求b1的值;
(2)求证数列{bnbn+1bn+2+n}是等差数列;
(3)设数列{Tn}满足:Tn+1=Tnbn+1(n∈N*),且T1=b1=-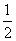 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列有关命题的说法正确的是( )
A.命题“若x2 =4,则x=2”的否命题为:“若x2 =4,则x≠2”
B.“x=2”是“x2—6x+8=0”的必要不充分条件
C.命题“若x=y,则cosx=cosy”的逆否命题为真命题
D.命题“存在x∈R,使得x2+x+3>0”的否定是:“对于任意的x∈R,均有
x2 +x+3<0"
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com