
分析 (1)由根式内部的代数式大于等于0求解不等式得到集合A;
(2)求解一元二次不等式化简集合B,分类讨论,利用B∩A=B得到B是A的子集,然后利用端点值间的关系列不等式求解a的取值范围.
解答 解:(1)由x2-1≥0,得x≤-1或x≥1,即A=(-∞,-1]∪[1,+∞);
(2)由(x-a-1)(2a-x)>0,得(x-a-1)(x-2a)<0.
∵a<1时,∴a+1>2a,∴B=(2a,a+1).
∵A∩B=B,∴B⊆A,∴2a≥1或a+1≤-1,即a≥$\frac{1}{2}$或a≤-2.
而a<1,∴$\frac{1}{2}$≤a<1或a≤-2.
a=1,B=∅,满足题意;
a>1时,B=(a+1,2a).
∵A∩B=B,∴B⊆A,∴a+1≥1或2a≤-1,即a≥0或a≤-$\frac{1}{2}$.
而a>1,∴a>1.
综上所述,实数a的取值范围是a≥$\frac{1}{2}$或a≤-2.
点评 本题考查了一元二次不等式的解法,考查了交集及其运算,解答的关键在于对端点值的取舍,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 3$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 家庭编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,0,1) | (1,2,1) | (1,2,2) | (1,1,1) | (1,2,2) | (1,2,1) | (1,1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
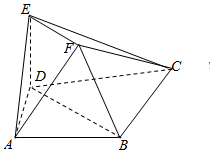 梯形BDEF所在平面垂直于平面ABCD于BD,EF∥BD,EF=DE=$\frac{1}{2}$BD,BD=BC=CD=$\sqrt{2}$AB=$\sqrt{2}$AD=2,DE⊥BC.
梯形BDEF所在平面垂直于平面ABCD于BD,EF∥BD,EF=DE=$\frac{1}{2}$BD,BD=BC=CD=$\sqrt{2}$AB=$\sqrt{2}$AD=2,DE⊥BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com