Question

17．当x≥2时，2^-x＜log_ax，则实数a的取值范围是（1，16）．

Answer 1

分析 由题意画出函数${y}_{1}={2}^{-x}，{y}_{2}=lo{g}_{a}x$的图象，求出y=log_ax经过点（2，$\frac{1}{4}$）时的a值，则满足条件的实数a的取值范围可求．

解答 解：令${y}_{1}={2}^{-x}，{y}_{2}=lo{g}_{a}x$，
作出函数图象如图，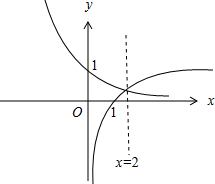

当x≥2时，2^-x＞0，
若0＜a＜1，则x≥2时，log_ax＜0，不等式不成立，∴a＞1，
∵${y}_{1}={2}^{-x}，{y}_{2}=lo{g}_{a}x$交于（2，$\frac{1}{4}$）时a=16，
∴要使当x≥2时，2^-x＜log_ax成立，则1＜a＜16．
∴实数a的取值范围是（1，16）．
故答案为：（1，16）．

点评 本题以指数函数与对数函数图象与性质为载体考查了函数恒成立问题，其中熟练掌握指数函数和对数函数的图象与性质是解答本题的关键，是中档题．