【题目】某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程
，其中
， 
；
(2)预计在今后的销售中，销量与单价仍然服从(1)中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？(利润＝销售收入－成本)
【答案】（1）
＝－20x＋250.（2）8.25
【解析】试题分析：（1）计算
，根据回归直线方程过样本中心点求出a的值，写出回归直线方程；
（2）设工厂获得的利润为L元，利用回归直线方程写出L的利润函数，求出最大值即可．
试题解析：
解：(1)由于
＝
(8＋8.2＋8.4＋8.6＋8.8＋9)＝8.5，
＝ (90＋84＋83＋80＋75＋68)＝80.
所以
=-20,
＝－＝80＋20×8.5＝250，
从而回归直线方程为
＝－20x＋250.
(2)设工厂获得的利润为L元，依题意得
L＝x(－20x＋250)－4(－20x＋250)
＝－20x2＋330x－1 000
＝－20
2＋361.25.
当且仅当x＝8.25时，L取得最大值．
故当单价定为8.25元时，工厂可获得最大利润．
寒假乐园北京教育出版社系列答案科目：高中数学 来源： 题型：
【题目】已知正项数列{an}，其前n项和Sn满足6Sn=an2+3an+2，且a1 ， a2 ， a6是等比数列{bn}的前三项．
（1）求数列{an}与{bn}的通项公式；
（2）记Tn=a1b1+a2b2+…+anbn ， n∈N*，求Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，正方形ABCD的边长为2 
，四边形BDEF是平行四边形，BD与AC交于点G，O为GC的中点，且FO⊥平面ABCD，FO= 
． 
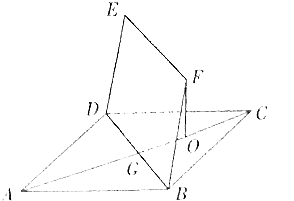
（1）求BF与平面ABCD所成的角的正切值；
（2）求三棱锥O﹣ADE的体积；
（3）求证：平面AEF⊥平面BCF．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设某大学的女生体重y(单位：kg)与身高x(单位：cm)具有线性相关关系，根据一组样本数据(xi，yi)(i＝1,2，…，n)，用最小二乘法建立的回归方程为
＝0.85x－85.71，则下列结论中不正确的是( )
A. y与x具有正的线性相关关系
B. 若给变量x一个值，由回归直线方程
＝0.85x－85.71得到一个
，则
为该统计量中的估计值
C. 若该大学某女生身高增加1 cm，则其体重约增加0.85 kg
D. 若该大学某女生身高为170 cm，则可断定其体重必为58.79 kg
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某居民区随机抽取10个家庭，获得第i个家庭的月收入xi(单位：千元)与月储蓄yi(单位：千元)的数据资料，算得 ＝80， ＝20， i＝184， ＝720.
(1)求家庭的月储蓄y对月收入x的线性回归方程
；
(2)判断变量x与y之间是正相关还是负相关；
(3)若该居民区某家庭月收入为7千元，预测该家庭的月储蓄．
附：线性回归方程
中， 
，其中
为样本平均值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的前
项和为
， 
，数列
满足
点
在直线
上.
(1)求数列
， 
的通项
， 
；
(2)令
，求数列
的前
项和
；
(3)若
，求对所有的正整数
都有
成立的
的范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，ABCD﹣A1B1C1D1是棱长为a的正方体，M、N分别是下底面的棱A1B1 ， B1C1的中点，P是上底面的棱AD上的一点，AP= 
，过P、M、N的平面交上底面于PQ，Q在CD上，则PQ= ．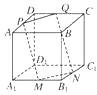 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
