
分析 延长F1P,与F2A的延长线交于M点,连接AO,根据等腰三角形“三线合一”和三角形中位线定理,结合椭圆的定义证出OA的长恰好等于椭圆的长半轴a,即a=2b,运用a,b,c的关系和离心率公式,计算即可得到所求值.
解答 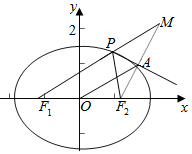 解:由题意,延长F1P,与F2A的延长线交于M点,连接AO,
解:由题意,延长F1P,与F2A的延长线交于M点,连接AO,
由PA是∠F2PM的平分线,且PA⊥MF2;
可得△F2MP中,|PF2|=|PM|且A为MF2的中点,
由三角形中位线定理,得|OA|=$\frac{1}{2}$|MF1|=$\frac{1}{2}$(|MP|+|PF1|)
由椭圆的定义,得|PF1|+|PF2|=2a,(2a是椭圆的长轴),
可得|MP|+|PF1|=2a,
即有|OA|=$\frac{1}{2}$(|MP|+|PF1|)=a,
由|OA|=2b,可得a=2b,即b=$\frac{1}{2}$a,
可得c=$\sqrt{{a}^{2}-{b}^{2}}$=$\frac{\sqrt{3}}{2}$a,
则e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查椭圆的离心率的求法,着重考查了椭圆的定义、等腰三角形的判定和三角形中位线定理等知识,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | -$\frac{3}{4}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
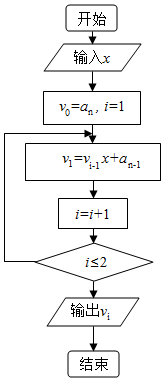 我国古代秦九韶算法可计算多项式anxn+an-1xn-1+…+a1x+a0的值,它所反映的程序框图如图所示,当x=1时,当多项式为x4+4x3+6x2+4x+1的值为( )
我国古代秦九韶算法可计算多项式anxn+an-1xn-1+…+a1x+a0的值,它所反映的程序框图如图所示,当x=1时,当多项式为x4+4x3+6x2+4x+1的值为( )| A. | 5 | B. | 16 | C. | 15 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (2,+∞) | C. | (-∞,1)∪(1,2) | D. | (-∞,1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 20 | C. | 26 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$+$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com