Question

19．在△ABC中，|$\overrightarrow{BC}$|=1，$\overrightarrow{BA}$•$\overrightarrow{BC}$=2，点P为线段BC上的动点，则（$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$）•$\overrightarrow{PB}$的最小值为（　　）

• A． -$\frac{1}{4}$
• B． -$\frac{3}{4}$
• C． -$\frac{1}{2}$
• D． -$\frac{3}{2}$

Answer 1

分析 由题意画出图形，结合|$\overrightarrow{BC}$|=1，$\overrightarrow{BA}$•$\overrightarrow{BC}$=2，可得$\overrightarrow{BA}cos∠ABC=2$，设$|\overrightarrow{PB}|=t$，展开（$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$）•$\overrightarrow{PB}$，化为含有t的函数式，再利用配方法求得最值．

解答 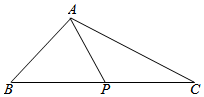解：如图，
（$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$）•$\overrightarrow{PB}$=$\overrightarrow{PA}•\overrightarrow{PB}+{\overrightarrow{PB}}^{2}+\overrightarrow{PC}•\overrightarrow{PB}$．
∵|$\overrightarrow{BC}$|=1，$\overrightarrow{BA}$•$\overrightarrow{BC}$=2，
∴$\overrightarrow{BA}cos∠ABC=2$，设$|\overrightarrow{PB}|=t$，
则$|\overrightarrow{PC}|=1-t$，
∴（$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$）•$\overrightarrow{PB}$=-2t+t²+t²-t（1-t）=3t²-3t
=$3（t-\frac{1}{2}）^{2}-\frac{3}{4}$．
∴当t=$\frac{1}{2}$时，（$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$）•$\overrightarrow{PB}$有最小值$-\frac{3}{4}$．
故选：B．

点评 本题考查平面向量的数量积运算，考查数学转化思想方法，训练了利用配方法求最值，是中档题．