
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{6}{7}$ |
分析 根据等边三角形的性质,分别求出任取两个点间的距离,然后求出这7个点中任取两个点的所有种数,找到满足两点间的距离小于1的种数,根据概率公式计算即可.
解答  解:如图,△ABC为等边三角形,D,E,F分别为BC,AC,AB上中点,交点为O,
解:如图,△ABC为等边三角形,D,E,F分别为BC,AC,AB上中点,交点为O,
∴AB=BC=AC=2,AD=BE=CF=$\sqrt{3}$,EF=DE=DF=1,AE=CE=AF=BF=BD=CD=1,A0=BO=CO=$\frac{2\sqrt{3}}{3}$,OD=OE=OF=$\frac{\sqrt{3}}{3}$,
由这7个点中任取两个点共有C72=21种,其中这两点间的距离小于1只能是OD,OE,OF共三种,
故这两点间的距离小于1的概率是$\frac{3}{21}$=$\frac{1}{7}$,
故选:A.
点评 本题考查了等边三角形的性质,以及古典概率的问题,关键是求出每条线段的长度,属于基础题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
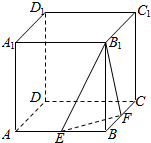 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
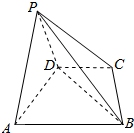 在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
在四棱锥P-ABCD 中,△PAD 为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,PD=AD=1,PD⊥底面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com