
分析 求出函数的导数,解关于导函数的不等式,由余弦函数的图象和性质,即可得到函数的单调区间,从而求出函数的极值,从而求出a,b的值.
解答 解:函数f(x)=xsinx+cosx+a,
f′(x)=sinx+xcosx-sinx=xcosx,
令f′(x)>0,即有xcosx>0,
即有 $\left\{\begin{array}{l}{x>0}\\{cosx>0}\end{array}\right.$或 $\left\{\begin{array}{l}{x<0}\\{cosx<0}\end{array}\right.$,
解得,x∈(0,$\frac{π}{2}$)或(2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$)((k为正整数)
或(2kπ+$\frac{π}{2}$,2kπ+$\frac{3π}{2}$)(k为负整数).
由于x∈(-π,π),则增区间为(0,$\frac{π}{2}$),(-π,-$\frac{π}{2}$),
同理解得,减区间为($\frac{π}{2}$,π),(-$\frac{π}{2}$,0),
∴f(x)极小值=f(0)=cos0+a=0①,f(x)极大值=f(-$\frac{π}{2}$)=f($\frac{π}{2}$)=$\frac{π}{2}$+a=b②,
由①②解得:a=-1,b=$\frac{π}{2}$-1.
点评 本题考查导数的运用:求单调区间,考查三角函数的图象和性质,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
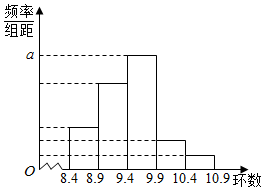 某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:
某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [8.4,8.9) | 9 | 0.15 |
| [8.9,9.4) | m | 0.3 |
| [9.4,9.9) | 24 | n |
| [9.9,10.4) | q | p |
| [10.4,10.9) | 3 | 0.05 |
| 合计 | t | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com