
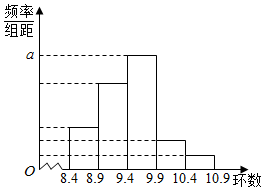
 某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:
某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [8.4,8.9) | 9 | 0.15 |
| [8.9,9.4) | m | 0.3 |
| [9.4,9.9) | 24 | n |
| [9.9,10.4) | q | p |
| [10.4,10.9) | 3 | 0.05 |
| 合计 | t | 1 |
分析 (Ⅰ)由频数与频率的统计表和频率分布直方图,能求出表中t,p及图中a的值.
(Ⅱ)由题意X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列及数学期望.
解答 解:(Ⅰ)由频数与频率的统计表和频率分布直方图,得:
$\frac{9}{t}=0.15$,解得t=60,
∴n=$\frac{24}{t}=\frac{24}{60}$=0.4,a=$\frac{0.4}{0.5}$=0.8.
∵0.15+0.3+n+p+0.05=1,∴p=0.1.
(Ⅱ)由直方图,得不少于9.9环的成绩的次数为60×0.15=9,
成绩不少于10.4环的次数为3,则X的可能取值为0,1,2,3,
P(X=0)=$\frac{{C}_{3}^{0}{C}_{6}^{3}}{{C}_{9}^{3}}$=$\frac{5}{21}$,
P(X=1)=$\frac{{C}_{3}^{1}{C}_{6}^{2}}{{C}_{9}^{3}}$=$\frac{15}{28}$,
P(X=2)=$\frac{{C}_{3}^{2}{C}_{6}^{1}}{{C}_{9}^{3}}$=$\frac{3}{14}$,
P(X=3)=$\frac{{C}_{3}^{3}{C}_{6}^{0}}{{C}_{9}^{3}}$=$\frac{1}{84}$,
∴随机变量X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{5}{21}$ | $\frac{15}{28}$ | $\frac{3}{14}$ | $\frac{1}{84}$ |
点评 本题考查频率直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
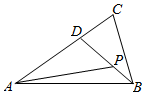 如图,在△ABC中,$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AC}$,$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{BD}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则下列关于λ,μ的值说法正确的是( )
如图,在△ABC中,$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AC}$,$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{BD}$,若$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则下列关于λ,μ的值说法正确的是( )| A. | λ=$\frac{2}{3}$ | B. | λ=$\frac{1}{3}$ | C. | μ=$\frac{4}{9}$ | D. | μ=$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com