
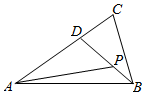
 ШчЭМЃЌдкЁїABCжаЃЌ$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AC}$ЃЌ$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{BD}$ЃЌШє$\overrightarrow{AP}$=ІЫ$\overrightarrow{AB}$+ІЬ$\overrightarrow{AC}$ЃЌдђЯТСаЙигкІЫЃЌІЬЕФжЕЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкЁїABCжаЃЌ$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AC}$ЃЌ$\overrightarrow{BP}$=$\frac{1}{3}$$\overrightarrow{BD}$ЃЌШє$\overrightarrow{AP}$=ІЫ$\overrightarrow{AB}$+ІЬ$\overrightarrow{AC}$ЃЌдђЯТСаЙигкІЫЃЌІЬЕФжЕЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ| AЃЎ | ІЫ=$\frac{2}{3}$ | BЃЎ | ІЫ=$\frac{1}{3}$ | CЃЎ | ІЬ=$\frac{4}{9}$ | DЃЎ | ІЬ=$\frac{1}{3}$ |
ЗжЮі ИљОнЯђСПЯпаддЫЫуЕФМИКЮвтвхгУ$\overrightarrow{AB}ЃЌ\overrightarrow{AC}$БэЪОГі$\overrightarrow{AP}$ЃЌЧѓГіІЫЃЌІЬЃЎ
НтД№ НтЃК$\overrightarrow{BP}=\frac{1}{3}\overrightarrow{BD}=\frac{1}{3}ЃЈ\overrightarrow{AD}-\overrightarrow{AB}ЃЉ$=$\frac{1}{3}ЁС\frac{2}{3}\overrightarrow{AC}-\frac{1}{3}\overrightarrow{AB}$=$\frac{2}{9}\overrightarrow{AC}-\frac{1}{3}\overrightarrow{AB}$ЃЎ
$\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{BP}$=$\frac{2}{3}\overrightarrow{AB}+\frac{2}{9}\overrightarrow{AC}$ЃЎ
ЁрІЫ=$\frac{2}{3}$ЃЌІЬ=$\frac{2}{9}$ЃЎ
ЙЪбЁЃКAЃЎ
ЕуЦР БОЬтПМВщСЫЦНУцЯђСПЕФЯпаддЫЫуЕФМИКЮвтвхЃЌЦНУцЯђСПЕФЛљБОЖЈРэЃЌЪєгкЛљДЁЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
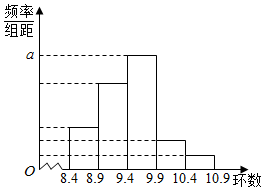 ФГЩфЛїбЕСЗЛљЕиНЬСЗЮЊСЫЖдФГдЫЖЏдБЕФГЩМЈзівЛЗжЮіЃЌЫцЛњГщШЁИУУћдЫЖЏдБЕФtДЮЩфЛїГЩМЈзїЮЊвЛИібљБОЃЌИљОнДЫЪ§ОнзіГіСЫЦЕЪ§гыЦЕТЪЕФЭГМЦБэКЭЦЕТЪЗжВМжБЗНЭМШчЯТЃК
ФГЩфЛїбЕСЗЛљЕиНЬСЗЮЊСЫЖдФГдЫЖЏдБЕФГЩМЈзівЛЗжЮіЃЌЫцЛњГщШЁИУУћдЫЖЏдБЕФtДЮЩфЛїГЩМЈзїЮЊвЛИібљБОЃЌИљОнДЫЪ§ОнзіГіСЫЦЕЪ§гыЦЕТЪЕФЭГМЦБэКЭЦЕТЪЗжВМжБЗНЭМШчЯТЃК| Зжзщ | ЦЕЪ§ | ЦЕТЪ |
| [8.4ЃЌ8.9ЃЉ | 9 | 0.15 |
| [8.9ЃЌ9.4ЃЉ | m | 0.3 |
| [9.4ЃЌ9.9ЃЉ | 24 | n |
| [9.9ЃЌ10.4ЃЉ | q | p |
| [10.4ЃЌ10.9ЃЉ | 3 | 0.05 |
| КЯМЦ | t | 1 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | [-1ЃЌ+ЁоЃЉ | BЃЎ | ЃЈ1ЃЌ+ЁоЃЉ | CЃЎ | [1ЃЌ+ЁоЃЉ | DЃЎ | ЃЈ-1ЃЌ+ЁоЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | Ђл | BЃЎ | ЂйЂк | CЃЎ | ЂйЂкЂл | DЃЎ | ЂйЂкЂлЂм |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com