
分析 (1)根据f(x)为定义在R上的奇函数,从而有f(0)=0,这样便可求出k=-1,从而$f(x)={2}^{x}-\frac{1}{{2}^{x}}$,根据指数函数的单调性和增函数的定义即可判断出f(x)为R上的增函数;
(2)可求出f(1)=$\frac{3}{2}$,从而有f(x)>f(1),根据f(x)的单调性便可得出f(x)$>\frac{3}{2}$的解集,即x的取值范围;
(3)先得到g(x)=22x+2-2x+2m(2x-2-x),可设2x-2-x=t,并可得到$t∈[\frac{3}{2},+∞)$,从而有h(t)=t2+2mt+2,对称轴为t=-m,从而可以讨论-m和$\frac{3}{2}$的关系:分$-m≤\frac{3}{2}$和$-m>\frac{3}{2}$两种情况,求出每种情况下的h(t)的最小值,根据最小值为-2即可求出m的值.
解答 解:(1)f(x)为R上的奇函数;
∴f(0)=1+k=0;
∴k=-1;
∴$f(x)={2}^{x}-\frac{1}{{2}^{x}}$;
x增大时,2x增大,$\frac{1}{{2}^{x}}$减小,$-\frac{1}{{2}^{x}}$增大;
∴${2}^{x}-\frac{1}{{2}^{x}}$增大,即f(x)增大;
∴f(x)在R上单调递增;
(2)由(1)f(x)在R上单调递增,且f(1)=$\frac{3}{2}$;
∴$f(x)>\frac{3}{2}$的解集为(1,+∞);
(3)g(x)=22x+2-2x+2m(2x-2-x);
令2x-2-x=t,则22x+2-2x=t2+2,由x∈[1,+∞)得t$∈[\frac{3}{2},+∞)$;
∴h(t)=t2+2mt+2=(t+m)2+2-m2,$t∈[\frac{3}{2},+∞)$;
①当$-m≤\frac{3}{2}$,即$m≥-\frac{3}{2}$时,h(t)在$[\frac{3}{2},+∞)$上为增函数;
∴$h(t)_{min}=h(\frac{3}{2})=\frac{9}{4}+3m+2=-2$,解得$m=-\frac{25}{12}∉(-\frac{3}{2},+∞)$(舍去);
②当$-m>\frac{3}{2}$,即$m<-\frac{3}{2}$时,$h(t)_{min}=h(-m)=2-{m}^{2}=-2$,解得m=-2,或m=2(舍去);
∴综上可得,m的值为-2.
点评 考查奇函数的定义,奇函数在原点有定义时,原点处的函数值为0,以及增函数的定义,指数函数的单调性,根据增函数的定义解不等式的方法,换元法的运用,以及二次函数的对称轴,二次函数的单调性,二次函数的最小值的求法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow a•\overrightarrow b>0$,则△ABC为钝角三角形 | B. | $\overrightarrow a•\overrightarrow b=0$,则△ABC为直角三角形 | ||
| C. | $\overrightarrow a•\overrightarrow b=\overrightarrow b•\overrightarrow c$,则△ABC为等腰三角形 | D. | $\overrightarrow c•({\overrightarrow a+\overrightarrow b+\overrightarrow c})=0$,则△ABC为正三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | (1,2] | C. | [1,2] | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100 | B. | 1024 | C. | 1022 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
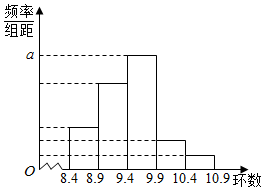 某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:
某射击训练基地教练为了对某运动员的成绩做一分析,随机抽取该名运动员的t次射击成绩作为一个样本,根据此数据做出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [8.4,8.9) | 9 | 0.15 |
| [8.9,9.4) | m | 0.3 |
| [9.4,9.9) | 24 | n |
| [9.9,10.4) | q | p |
| [10.4,10.9) | 3 | 0.05 |
| 合计 | t | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com