
分析 根据$f(\frac{π}{4}+x)=f(\frac{π}{4}-x)$,得出x=$\frac{π}{4}$是函数f(x)的一条对称轴,从而求出φ的表达式,再函数g(x)的解析式以及$g(\frac{π}{4})$的值.
解答 解:∵函数f(x)=2cos(ωx+φ)对任意的x都有$f(\frac{π}{4}+x)=f(\frac{π}{4}-x)$,
∴x=$\frac{π}{4}$是函数f(x)的一条对称轴,
∴cos($\frac{π}{4}$ω+φ)=±1,
即$\frac{π}{4}$ω+φ=kπ,k∈Z,
∴φ=kπ-$\frac{π}{4}$ω,k∈Z;
∴函数g(x)=3sin(ωx+φ)-1=3sin(ωx+kπ-$\frac{π}{4}$ω)-1,k∈Z;
∴$g(\frac{π}{4})$=3sin($\frac{π}{4}$ω+kπ-$\frac{π}{4}$ω)=3sinkπ-1=-1.
故答案为:-1.
点评 本题主要考查三角函数的对称轴的问题.注意正余弦函数在其对称轴上取最值,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
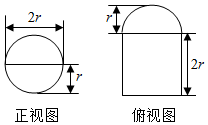 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图 中的正视图和俯视图如图所示,若 该几何体的表面积为64+80π,则 r=( )
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图 中的正视图和俯视图如图所示,若 该几何体的表面积为64+80π,则 r=( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-6,0) | B. | [-6,0] | C. | (-1,0] | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\root{3}{V}$ | B. | $\root{3}{\frac{V}{π}}$ | C. | $\root{3}{4V}$ | D. | $\root{3}{\frac{V}{2π}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{5}{2}$ | C. | $\frac{2}{5}$ | D. | $-\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | “a<b”是“a+c<b+c”的充要条件 | |
| D. | 命题$p:?{x_0}∈R,{e^{x_0}}≤0$为假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com