已知点F(1,0),直线l:x=-1,动点P到点F的距离等于点P到直线l的距离,动直线PO与直线l交于动点N,过N且平行于x轴的直线与动直线PF交于动点Q.
(Ⅰ)求证:动点P、Q在同一条曲线C上运动;
(Ⅱ)曲线C在点P处的切线与直线l交于点R,M为线段PQ的中点.
(1)求证:直线RM∥x轴;
(2)若直线RM平分∠PRF,求直线PQ的方程.
【答案】
分析:(Ⅰ)根据抛物线的定义,可判断P点在抛物线y
2=4x上,所以要想证明动点P、Q在同一条曲线C上运动,只需证明Q点也在抛物线y
2=4x上即可,利用Q点为过N且平行于x轴的直线与动直线PF的交点,带着参数求出Q点坐标,证明不论参数为何值,Q点都满足抛物线y
2=4x方程,就可证明在抛物线y
2=4x上.
(Ⅱ)(1)欲证直线RM∥x轴,只需证明R,M两点的纵坐标相等.利用导数求出抛物线在P点处的切线斜率,得到切线方程,再与直线l:x=-1联立,解出R点坐标,用中点坐标公式求出M点坐标,观察纵坐标是否相同即可.
(2)由于直线RM平分∠PRF,且RM∥x轴,可得几何条件|AR|=|RF|,由(1)中直线PR的方程,表示出R点坐标,依几何条件列方程可求得点P的坐标,最后由两点式写出所求直线方程
解答:解:(I)点P在曲线C:y
2=4x上
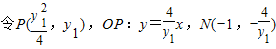
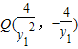
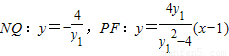
将直线NQ的方程代入直线PF的方程消去y
1,得y
2=4x
∴点Q在曲线C上.
(II)
(1)∵
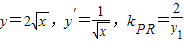
∴
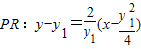
∴
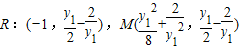
显然RM∥x轴

若RM平分∠PRF,且RM∥x轴
∴|AR|=|RF|
即
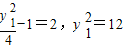
∵
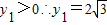
∴P(3,2
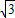
),又F(1,0)
∴
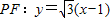
即直线PQ的方程为
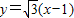 点评:
点评:本题综合考察了抛物线的标准方程和几何性质,直线与抛物线的关系,解题时要学会通过恰当设点的坐标进行证明和计算,要学会将几何条件进行转化,便于证明和计算

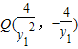
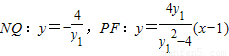
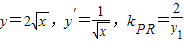
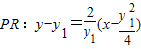
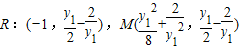

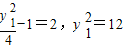
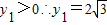
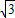 ),又F(1,0)
),又F(1,0)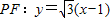


 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若