
已知数列 中,
中,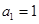 ,
, ,数列
,数列 中,
中,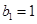 ,且点
,且点 在直线
在直线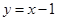 上.
上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)若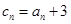 ,求数列
,求数列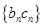 的前项和
的前项和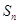 .
.
(Ⅰ)  ;(Ⅱ)
;(Ⅱ)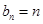 ;(Ⅲ)
;(Ⅲ)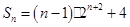 .
.
解析试题分析:(Ⅰ) 由已知可构造数列 ,并证明其为等比数列,先求出数列
,并证明其为等比数列,先求出数列 的通项公式,再求数列
的通项公式,再求数列 的通项公式(一般形如
的通项公式(一般形如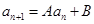 的递推关系,可先构造等比数列
的递推关系,可先构造等比数列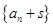 ,其公比
,其公比 与常数
与常数 ,可由
,可由 与所给等式
与所给等式 进行比较求得);(Ⅱ)将点
进行比较求得);(Ⅱ)将点 代入直线方程
代入直线方程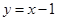 ,可得到数列
,可得到数列 中
中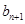 与
与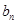 的关系式,从而发现
的关系式,从而发现 为等差数列,即可求出数列
为等差数列,即可求出数列 的通项公式;(Ⅲ)由(Ⅰ) (Ⅱ)可得数列
的通项公式;(Ⅲ)由(Ⅰ) (Ⅱ)可得数列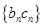 的通项公式,观察
的通项公式,观察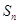 中各项关系,可用错位相减法来求出
中各项关系,可用错位相减法来求出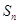 (错位相减法是求数列前项
(错位相减法是求数列前项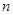 和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
和的常用方法,它适用于如果一个数列的各项是由一个等差数列和一个等比数列的对应各项之积构成的).
试题解析:(Ⅰ)由 得
得
所以 是首项为
是首项为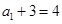 ,公比为2的等比数列.
,公比为2的等比数列.
所以 ,故
,故
(Ⅱ)因为 在直线
在直线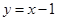 上,
上,
所以 即
即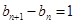 又
又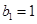
故数列 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
所以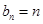
(Ⅲ)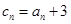 =
=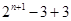 =
=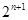 故
故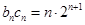
所以
故
相减得
所以
考点:1.等比数列;2.等差数列;3.数列前项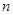 和求法.
和求法.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
等差数列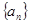 中,
中,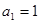 ,公差
,公差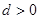 ,且它的第2项,第5项,第14项分别是等比数列
,且它的第2项,第5项,第14项分别是等比数列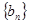 的第2项,第3项,第4项.
的第2项,第3项,第4项.
(Ⅰ)求数列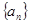 与
与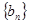 的通项公式;
的通项公式;
(Ⅱ)设数列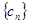 对任意自然数均有
对任意自然数均有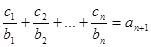 成立,求
成立,求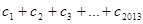 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com