
非零向量 =a,
=a, 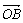 =b,若点B关于
=b,若点B关于 所在直线的对称点为B1,则向量
所在直线的对称点为B1,则向量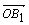 为 ( )
为 ( )
A.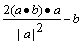 B.2a-b C.
B.2a-b C.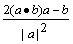 D.
D.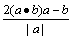
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
到直线2x+y+1=0的距离为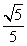 的点的集合是( )
的点的集合是( )
A.直线2x+y-2=0 B.直线2x+y=0
C.直线2x+y=0或直线2x+y-2=0 D.直线2x+y=0或直线2x+y+2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标平面中,已知点P1(1,2),P2(2,22),P3(3,23)…,Pn(n,2n),其中n是正整数,对平面上任一点Ao,记A1为Ao关于点P1的对称点,A2为A1,关于点P2的对称点,…,An为An-1关于点Pn的对称点.
(1)求向量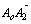 的坐标;
的坐标;
(2)当点Ao在曲线C上移动时.点A2的轨迹是函数y=f(x)的图像,其中f(x)是以3为周期的周期函数,且当x∈(0,3)时f(x)=lgx.求以曲线C为图像的函数在(1,4)上的解析式;
(3)对任意偶数n,用n表示向量 的坐
的坐 标.
标.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A(-2,0), B(2,0),点C、D满足
B(2,0),点C、D满足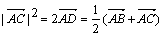
(1)求D的轨迹;
(2)过点A作直线l交以A、B为焦点的椭圆于M、N 两点,线段MN的中点到了轴的距 离为
离为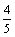 ,且l与D的轨迹相切,求椭圆方程.
,且l与D的轨迹相切,求椭圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
对于0<a<1,给出下列四个不等式
①loga(1+o)<loga(1+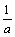 ) ②1oga(1+o)>loga(1+
) ②1oga(1+o)>loga(1+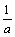 ) ③a1+a<a
) ③a1+a<a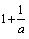 ④a1+a>a
④a1+a>a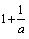
其中成立的是 ( )
A.①与③ B.①与④ C.②与③ D.②与④
查看答案和解析>>
科目:高中数学 来源: 题型:
若椭圆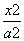 +
+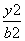 =1的焦点在x轴上,过点(1,
=1的焦点在x轴上,过点(1,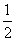 )作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________________.
)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com