
分析 先将问题转化成二项式的展开式中没有常数项,利用二项展开式的通项公式求出第r+1项,令x的指数为2时方程无解,检验求得n的值.
解答 解:∵(x+1)2(x+$\frac{1}{{x}^{3}}$)n=(1+2x+x2)(x+$\frac{1}{{x}^{3}}$)n 的展开式中没有x2项,
∴(x+$\frac{1}{{x}^{3}}$)n 的展开式中不含常数项,不含x项,不含x2项.
∵(x+$\frac{1}{{x}^{3}}$)n 的展开式中展开式的通项为Tr+1=Cnr xn-r x-3r=Cnrxn-4r,r=0,1,2,3…n,
方程n-4r=0,n-4r=1,n-4r=2,当n∈N*,5≤n≤8时,无解,检验可得n=7,
故答案为:7.
点评 本题考查数学中的等价转化的能力和利用二项展开式的通项公式解决二项展开式的特定项,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 144 | B. | 192 | C. | 228 | D. | 264 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{2}$ | B. | $\frac{\sqrt{65}}{8}$ | C. | $\frac{8\sqrt{7}}{21}$ | D. | $\frac{\sqrt{35}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
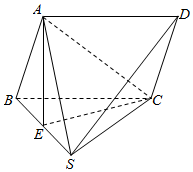 如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,平面ABS⊥平面CBS,侧面SBC是正三角形,AB=AS,点E是SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是平行四边形,平面ABS⊥平面CBS,侧面SBC是正三角形,AB=AS,点E是SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2${\;}^{-\frac{1}{3}}$,1) | B. | (0,2${\;}^{-\frac{1}{3}}$] | C. | (2${\;}^{\frac{1}{3}}$,3) | D. | (1,2${\;}^{\frac{1}{3}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P?Q?R | B. | P?R?Q | C. | Q?P?R | D. | R?P?Q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com