
| A. | P?Q?R | B. | P?R?Q | C. | Q?P?R | D. | R?P?Q |
分析 先确定P?Q,排除C,D,再确定Q?R,即可得出结论.
解答 解:集合P={(x,y)||x|+|y|≤1,x∈R,y∈R}表示以(±1,0),(0,±1)为顶点的正方形,
Q={(x,y)|x2+y2≤1,x∈R,y∈R}表示以(0,0)为圆心,1为半径的圆面(包括圆的边界),所以P?Q,排除C,D;
x4+y2≤1中,以$\sqrt{x}$代替x,可得x2+y2≤1,∴Q⊆R.
x=$\frac{1}{2}$,由x2+y2≤1,可得-$\frac{\sqrt{3}}{2}$≤y≤$\frac{\sqrt{3}}{2}$,由x4+y2≤1可得-$\frac{\sqrt{15}}{4}$≤y≤$\frac{\sqrt{15}}{4}$,∴Q?R
∴P?Q?R,
故选:A.
点评 本题考查集合的包含关系,考查学生的计算能力,比较基础.


科目:高中数学 来源: 题型:解答题
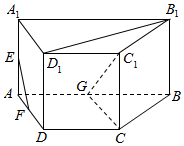 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AD=DC=AA1=2,AB=4,E、F、G分别是棱AA1、AD、AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AD=DC=AA1=2,AB=4,E、F、G分别是棱AA1、AD、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
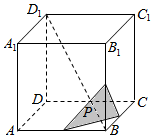 如图,在正方体ABCD-A1B1C1D1中,AB=1,点P为BD1上一点,平面α满足:点P∈平面α,直BD1⊥平面α,设以B为顶点,以连接平面α与正方体棱的交点为底面的几何体的体积为V,则V的最大值为( )
如图,在正方体ABCD-A1B1C1D1中,AB=1,点P为BD1上一点,平面α满足:点P∈平面α,直BD1⊥平面α,设以B为顶点,以连接平面α与正方体棱的交点为底面的几何体的体积为V,则V的最大值为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{16}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=20×($\frac{1}{2}$)x | B. | f(x)=-6log3x+8 | C. | f(x)=x2-12x+19 | D. | f(x)=x2-7x+14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在PD、PC上,2PN=NC,PM=MD
如图,已四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在PD、PC上,2PN=NC,PM=MD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${A}_{8}^{8}$种 | B. | 3${A}_{7}^{7}$种 | C. | 3${A}_{6}^{6}$种 | D. | ${A}_{3}^{3}$${A}_{6}^{6}$种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com