
分析 (1)由题意求出p,代入抛物线方程得答案;
(2)由题意设A(x1,y1)(x1>0),B(x2,y2),C(x3,y3),D(x4,y4).结合抛物线的性质把点的坐标用x1,x3表示,写出两直线方程联立后求出交点坐标得答案;
(3)由两直线垂直可得$\overrightarrow{FA}•\overrightarrow{FC}=0$,整理得到x1x3+$\frac{{(x}_{1}{x}_{3})^{2}}{16}$-$\frac{({x}_{1}+{x}_{3})^{2}-2{x}_{1}{x}_{3}}{4}$+1=0,设x1x3=t(t>0),把x1+x3用t表示,代入交点横坐标后,利用基本不等式求出x2≥0,从而可得直线AC,BD的交点横坐标范围.
解答 (1)解:由抛物线x2=2py的焦点F到准线的距离为2,得p=2,
∴抛物线方程为:x2=4y;
(2)证明:由题意设A(x1,y1)(x1>0),B(x2,y2),
C(x3,y3),D(x4,y4).
则${y}_{1}=\frac{{{x}_{1}}^{2}}{4},{y}_{2}=\frac{{{x}_{2}}^{2}}{4},{y}_{3}=\frac{{{x}_{3}}^{2}}{4},{y}_{4}=\frac{{{x}_{4}}^{2}}{4}$,
且x1x2=-4,x3x4=-4,y1y2=1,y3y4=1.
∴A(${x}_{1},\frac{{{x}_{1}}^{2}}{4}$),B($-\frac{4}{{x}_{1}},\frac{4}{{{x}_{1}}^{2}}$),C(${x}_{3},\frac{{{x}_{3}}^{2}}{4}$),D($-\frac{4}{{x}_{3}},\frac{4}{{{x}_{3}}^{2}}$).
${k}_{AC}=\frac{\frac{{{x}_{3}}^{2}}{4}-\frac{{{x}_{1}}^{2}}{4}}{{x}_{3}-{x}_{1}}=\frac{{x}_{1}+{x}_{3}}{4}$,${k}_{BD}=\frac{\frac{4}{{{x}_{3}}^{2}}-\frac{4}{{{x}_{1}}^{2}}}{\frac{4}{{x}_{1}}-\frac{4}{{x}_{3}}}=-\frac{{x}_{1}+{x}_{3}}{{x}_{1}{x}_{3}}$.
∴AC所在直线方程为$y-\frac{{{x}_{1}}^{2}}{4}=\frac{{x}_{1}+{x}_{3}}{4}(x-{x}_{1})$,
BD所在直线方程为$y-\frac{4}{{{x}_{1}}^{2}}=-\frac{{x}_{1}+{x}_{3}}{{x}_{1}{x}_{3}}(x+\frac{4}{{x}_{1}})$,
两式联立解得:$\left\{\begin{array}{l}{x=\frac{{x}_{1}{x}_{3}-4}{{x}_{1}+{x}_{3}}}\\{y=-1}\end{array}\right.$.
∴直线AC,BD的交点在准线上;
(3)解:由题意可知:$\overrightarrow{FA}•\overrightarrow{FC}=0$,即$({x}_{1},\frac{{{x}_{1}}^{2}}{4}-1)•({x}_{3},\frac{{{x}_{3}}^{2}}{4}-1)=0$,
∴${x}_{1}{x}_{3}+(\frac{{{x}_{1}}^{2}}{4}-1)(\frac{{{x}_{3}}^{2}}{4}-1)=0$,
即x1x3+$\frac{{(x}_{1}{x}_{3})^{2}}{16}$-$\frac{{{x}_{1}}^{2}+{{x}_{3}}^{2}}{4}$+1=0,
则x1x3+$\frac{{(x}_{1}{x}_{3})^{2}}{16}$-$\frac{({x}_{1}+{x}_{3})^{2}-2{x}_{1}{x}_{3}}{4}$+1=0,
设x1x3=t(t>0),
则$t+\frac{{t}^{2}}{16}-\frac{({x}_{1}+{x}_{3})^{2}-2t}{4}+1=0$,
即$({x}_{1}+{x}_{3})^{2}=\frac{{t}^{2}+24t+16}{4}$.
∴${x}^{2}=\frac{(t-4)^{2}}{\frac{{t}^{2}+24t+16}{4}}=\frac{4({t}^{2}-8t+16)}{{t}^{2}+24t+16}$=$4-\frac{128}{t+\frac{16}{t}+24}$≥0.
上式当且仅当t=4时“=”成立.
∴x∈(-∞,+∞).
即直线AC,BD的交点横坐标范围是(-∞,+∞).
点评 本题主要考查了抛物线的应用,平面解析式的基础知识.考查了考生的基础知识的综合运用和知识迁移的能力和计算能力.训练了利用基本不等式求最值.难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
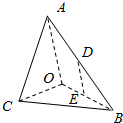 如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工作代码 | 紧前工作 | 工期(天) |
| A | 无 | 7 |
| B | 无 | 3 |
| C | 无 | 1 |
| D | C | 3 |
| E | A,B,D | 3 |
| F | E | 2 |
| G | A,B,D | 2 |
| H | F,G | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com