
分析 先求出函数的对称轴,通过讨论对称轴和区间的关系,得到方程,解出即可.
解答 解:∵y=$\frac{3}{4}$x2-3x+4=$\frac{3}{4}$(x-2)2+1,对称轴为x=2,分三种:
①轴在区间左边,2<a<b,
∴f(a)=a且f(b)=b,解得:a=$\frac{4}{3}$,b=4(舍)
②轴在区间右边,a<b<2,
∴f(a)=b且f(b)=a,解得:a=b=$\frac{4}{3}$(舍)
③轴在区间中间,a≤2≤b,
∴f(2)=a=1且f(b)=b,解得:a=1,b=4.
综上:a=1,b=4.
点评 本题考查了二次函数的性质,考查分类讨论思想,是一道基础题.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:2017届广东华南师大附中高三综合测试一数学(理)试卷(解析版) 题型:解答题
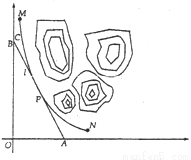
某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路.记两条相互垂直的公路为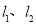 ,山区边界曲线为
,山区边界曲线为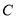 .计划修建的公路为
.计划修建的公路为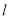 ,如图所示,
,如图所示,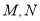 为
为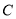 的两个端点,测得点
的两个端点,测得点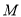 到
到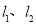 的距离分别为5千米和40千米,点
的距离分别为5千米和40千米,点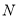 到
到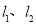 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以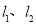 所在直线分别为
所在直线分别为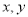 轴,建立平面直角坐标系
轴,建立平面直角坐标系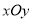 .假设曲线
.假设曲线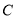 符合函数
符合函数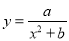 (其中
(其中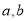 为常数)模型.
为常数)模型.
(1)求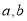 的值;
的值;
(2)设公路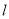 与曲线
与曲线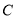 相切于
相切于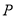 点,
点,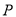 的横坐标为
的横坐标为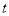 .
.
①请写出公路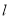 长度的函数解析式
长度的函数解析式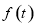 ,并写出其定义域;
,并写出其定义域;
②当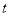 为何值时,公路
为何值时,公路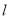 的长度最短?求出最短长度.
的长度最短?求出最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com