
分析 (1)由题设中所给的恒成立的等式对任意n∈N*都有(1-p)Sn=p-pan(p为大于1的常数),在此条件下求通项,一般利用an=Sn-Sn-1,故可构造出(1-p)Sn+1=p-pan+1.两式作差,即可消去和得到项之间的关系化简后再根据其形式判断规律求出通项;
(2)放小证明得出f(k)+f(2n-k)≥2f(n),由同向不等式相加证得结论.
解答 (1)解:∵(1-p)Sn=p-pan,①
∴(1-p)Sn+1=p-pan+1.②
②-①,得(1-p)an+1=-pan+1+pan,即an+1=pan.
在①中令n=1,可得a1=p.
∴{an}是首项为a1=p,公比为p的等比数列,${a_n}={p^n}$.
(2)证明:由(1)可得${S_n}=\frac{{p(1-{p^n})}}{1-p}=\frac{{p({p^n}-1)}}{p-1}$.$1+C_n^1{a_1}+C_n^2{a_2}+…+C_n^n{a_n}$
=$1+pC_n^1+{p^2}C_n^2+…+C_n^n{p^n}={(1+p)^n}={(p+1)^n}$.
∴$f(n)=\frac{{1+C_n^1{a_1}+C_n^2{a_2}+…+C_n^n{a_n}}}{{{2^n}{S_n}}}$=$\frac{p-1}{p}•\frac{{{{(p+1)}^n}}}{{{2^n}({p^n}-1)}}$,
当n≥2,k=1,2,…,2n-1时,$f(k)+f(2n-k)=\frac{p-1}{p}[{\frac{{{{(p+1)}^k}}}{{{2^k}({p^k}-1)}}+\frac{{{{(p+1)}^{2n-k}}}}{{{2^{2n-k}}({p^{2n-k}}-1)}}}]$$≥\frac{p-1}{p}•2\sqrt{\frac{{{{(p+1)}^k}}}{{{2^k}({p^k}-1)}}•\frac{{{{(p+1)}^{2n-k}}}}{{{2^{2n-k}}({p^{2n-k}}-1)}}}$=$\frac{p-1}{p}•\frac{{2{{(p+1)}^n}}}{2^n}\sqrt{\frac{1}{{({p^k}-1)({p^{2n-k}}-1)}}}$=$\frac{p-1}{p}•\frac{{2{{(p+1)}^n}}}{2^n}\sqrt{\frac{1}{{{p^{2n}}-{p^k}-{p^{2n-k}}+1}}}$.
∵pk+p2n-k≥2pn,∴p2n-pk-p2n-k+1≤p2n-2pn+1=(pn-1)2.
∴$f(k)+f(2n-k)≥\frac{p-1}{p}•\frac{{2{{(p+1)}^n}}}{{{2^n}({p^n}-1)}}=2f(n)$,(当且仅当k=n时取等号).
∴$\sum_{k=1}^{2n-1}{f(k)=}\frac{1}{2}\sum_{k=1}^{2n-1}{[f(k)+f(2n-k)]}≥\sum_{k=1}^{2n-1}{f(n)=}(2n-1)f(n)$.(当且仅当n=1时取等号).
综上所述,f(1)+f(2)+…+f(2n-1)≥(2n-1)f(n),(n∈N*).
点评 本题考查数列与不等式的综合,考查了数列递推式的应用,放缩法证明不等式,解题的关键是熟练掌握放缩法的技巧,需要有较高的观察能力与判断能力,既要放,又不能放得过了头,谨记.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
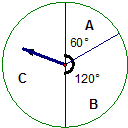 五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.| 指针位置 | A区域 | B区域 | C区域 |
| 返券金额(单位:元) | 60 | 30 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com