
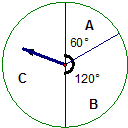
 五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.| 指针位置 | A区域 | B区域 | C区域 |
| 返券金额(单位:元) | 60 | 30 | 0 |
分析 (1)依题意知,ξ服从二项分布ξ~B(n,p),再由二项分布的期望公式与二项分布的方差公式可得方程组,进而求出p与n的值.
(2)设指针落在A,B,C区域分别记为事件A,B,C,再计算出P(A)=$\frac{1}{6}$,P(B)=$\frac{1}{3}$,P(C)=$\frac{1}{2}$,以及随机变量η的可能值为0,30,60,90,120,然后根据相互独立事件的概率乘法公式分布得到其发生的概率,假若求出离散型随机变量的分布列与期望.
解答 解:(1)依题意知,ξ服从二项分布ξ~B(n,p)
∴Eξ=np=$\frac{1}{25}$----------------①
又Dξ=(σξ)2=np(1-p)=$\frac{99}{2500}$----②
由①②联立解得:n=4,p=$\frac{1}{100}$;
(2)设指针落在A,B,C区域分别记为事件A,B,C.则P(A)=$\frac{1}{6}$,P(B)=$\frac{1}{3}$,P(C)=$\frac{1}{2}$.
由题意得,该顾客可转动转盘2次.
随机变量η的可能值为0,30,60,90,120.
P(η=0)=$\frac{1}{2}×\frac{1}{2}$=$\frac{1}{4}$
P(η=30)=$\frac{1}{2}×\frac{1}{3}×2$=$\frac{1}{3}$
P(η=90)=$\frac{1}{3}×\frac{1}{6}×2$=$\frac{1}{9}$
P(η=60)=$\frac{1}{2}×\frac{1}{6}×2$+$\frac{1}{3}×\frac{1}{3}$=$\frac{5}{18}$
P(η=120)=$\frac{1}{6}×\frac{1}{6}$=$\frac{1}{36}$.
所以,随机变量η的分布列为:
| P | 0 | 30 | 60 | 90 | 120 |
| η | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{5}{18}$ | $\frac{1}{9}$ | $\frac{1}{36}$ |
点评 解决此类问题的关键是熟练掌握二项分布的期望与方差公式与离散型随机变量的分布列、期望、方差,以及相互独立事件的概率乘法公式,此题属于中档题,是高考经常涉及的考点之一.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com