
分析 首先判断定义域是否关于原点对称,如果不对称,是非奇非偶的函数;如果对称,再由奇偶函数的定义判断.
解答 解:(1)f(x)=$\sqrt{{x}^{2}-4}$+$\sqrt{4-{x}^{2}}$的定义域为{x|x=±2},f(x)=0,f(-x)=f(x)=-f(x)=0,所以f(x)既是奇函数又是偶函数;
(2)f(x)=$\sqrt{x-4}$+$\sqrt{4-x}$的定义域为{x|x=4},关于原点不对称,是非奇非偶的函数;
(3)f(x)=$\frac{\sqrt{9-{x}^{2}}}{|x+3|-3}$定义域为{x|-3≤x≤3且x≠0},f(x)=$\frac{\sqrt{9-{x}^{2}}}{|x+3|-3}$=$\frac{\sqrt{9-{x}^{2}}}{x}$,f(-x)=-f(x),为奇函数;
(4)f(x)=$\left\{\begin{array}{l}{{x}^{2}+x-1}&{(x>0)}\\{-{x}^{2}+x+1}&{(x<0)}\end{array}\right.$定义域关于原点对称,x>0时f(-x)=-x2-x+1=-f(x);x<0时,f(-x)=(-x)2-x-1=-(-x2+x+1)=-f(x),所以为奇函数;
(5)f(x)=(x-1)$\sqrt{\frac{1+x}{1-x}}$,定义域为{x|-1≤x<1},关于原点不对称,是非奇非偶的函数.
点评 本题考查了函数奇偶性的判断;首先判断定义域是否关于原点对称,如果对称,再由奇偶函数的定义判断.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
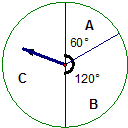 五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
五一节期间,某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券.(假定指针等可能地停在任一位置,指针落在区域的边界时,重新转一次)指针所在的区域及对应的返劵金额见右上表.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.| 指针位置 | A区域 | B区域 | C区域 |
| 返券金额(单位:元) | 60 | 30 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1)∪[2,3) | B. | [-1,2) | C. | (-∞,-1)∪[2,3)∪(3,+∞) | D. | (-∞,-1)∪(3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com