
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
分析 由基本不等式求最值可得f(x)在($\frac{1}{e},+∞$)大于2e,利用导数求出函数g(x)在($\frac{1}{e},+∞$)上的最大值为e,把对任意${x_1},{x_2}∈({\frac{1}{e},+∞})$,不等式$\frac{{g({x_1})}}{k}<\frac{{f({x_2})}}{k+2}$恒成立,转化为$\frac{e}{k}≤\frac{2e}{k+1}$,由此求得k的取值范围.
解答 解:∵当x>$\frac{1}{e}$时,f(x)=$\frac{{e}^{2}{x}^{2}+1}{x}$=${e}^{2}x+\frac{1}{x}$>2$\sqrt{{e}^{2}x+\frac{1}{x}}=2e$(x$≠\frac{1}{e}$).
∴x1∈($\frac{1}{e}$,+∞)时,函数f(x1)>2e;
∵g(x)=$\frac{{e}^{2}x}{{e}^{x}}$,∴g′(x)=$\frac{{e}^{2}({e}^{x}-x{e}^{x})}{{e}^{2x}}=\frac{{e}^{2}(1-x)}{{e}^{x}}$.
当$\frac{1}{e}$<x<1时,g′(x)>0,则函数g(x)在($\frac{1}{e}$,1)上单调递增,
当x>1时,g′(x)<0,则函数在(1,+∞)上单调递减.
∴当x=1时,函数g(x)有最大值g(1)=e.
则有x1、x2∈($\frac{1}{e}$,+∞)时,f(x1)>2e>g(x2)max=e.
∵不等式$\frac{{g({x_1})}}{k}<\frac{{f({x_2})}}{k+2}$恒成立且k>0,
∴$\frac{e}{k}≤\frac{2e}{k+1}$,得k≥1.
∴正数k的取值范围是[1,+∞).
故选:B.
点评 本题主要考查了利用基本不等式及导数求解函数的最值,考查函数的恒成立问题的转化,属中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
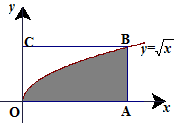 如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.
如图,长方形的四个顶点为O(0,2),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B.现将一质点随机投入长方形OABC中,则质点落在图中阴影区域的概率是$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com