
用数学归纳法证明: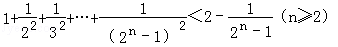 (n∈N*)时第一步需要证明( )
(n∈N*)时第一步需要证明( )
A.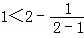
B.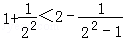
C.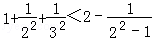
D.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.4一次同余方程练习卷(解析版) 题型:选择题
(2012•贵溪市模拟)设a、b、β为整数(β>0),若a和b被β除得的余数相同,则称a和b对β同余,记为a=b(modβ),已知a=1+C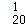 +C
+C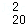 •2+C
•2+C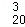 •22+…+C
•22+…+C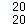 •219,b=a(mod10),则b的值可以是( )
•219,b=a(mod10),则b的值可以是( )
A.2010 B.2011 C.2012 D.2009
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:选择题
(2011•江西模拟)在算式“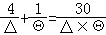 ”中,△、Θ都为正整数,且它们的倒数之和最小,则△、Θ的值分别为( )
”中,△、Θ都为正整数,且它们的倒数之和最小,则△、Θ的值分别为( )
A.6,6 B.10,5 C.14,4 D.18,3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例(解析版) 题型:解答题
(2011•河池模拟)已知正项数列{an}满足:a1=1,且(n+1)an+12=nan2﹣an+1an,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{ }的前n项积为Tn,求证:当x>0时,对任意的正整数n都有Tn>
}的前n项积为Tn,求证:当x>0时,对任意的正整数n都有Tn> .
.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
用数学归纳法证明“2n>n2+1对于n≥n0的自然数n都成立”时,第一步证明中的起始值n0应取( )
A.2 B.3 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
已知n为正偶数,用数学归纳法证明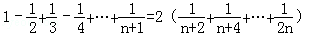 时,若已假设n=k(k≥2)为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立.
时,若已假设n=k(k≥2)为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立.
A.n=k+1 B.n=k+2 C.n=2k+2 D.n=2(k+2)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷(解析版) 题型:选择题
用反证法证明命题“如果a>b,那么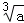 >
>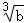 ”时,假设的内容是( )
”时,假设的内容是( )
A.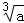 =
=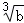 B.
B.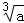 <
<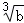
C.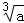 =
=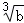 且
且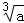 >
>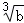 D.
D.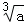 =
=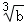 或
或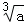 <
<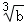
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com