已知n为正偶数，用数学归纳法证明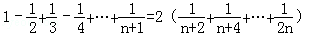
时，若已假设n=k（k≥2）为偶数）时命题为真，则还需要用归纳假设再证n=（ ）时等式成立．
A.n=k+1 B.n=k+2 C.n=2k+2 D.n=2（k+2）
科目：高中数学 来源：[同步]2014年新人教A版选修4-6 2.1同余练习卷（解析版） 题型：选择题
（2012•贵溪市模拟）设a、b、β为整数（β＞0），若a和b被β除得的余数相同，则称a和b对β同余，记为a=b（modβ），已知a=1+C
+C
•2+C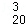
•22+…+C
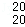•219，b=a（mod10），则b的值可以是（ ）
A.2010 B.2011 C.2012 D.2009
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.1整除练习卷（解析版） 题型：选择题
五进制数444（5）转化为八进制数是（ ）
A.194（8） B.233（8） C.471（8） D.174（8）
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例（解析版） 题型：选择题
用数学归纳法证明：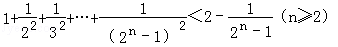
（n∈N*）时第一步需要证明（ ）
A.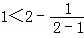
B.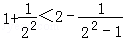
C.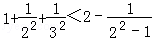
D.
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷（解析版） 题型：选择题
已知n为正偶数，用数学归纳法证明1﹣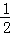
+
﹣
+…+
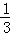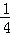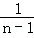=2（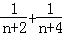
+…+
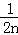）时，若已假设n=k（k≥2为偶数）时命题为真，则还需要用归纳假设再证（ ）
A.n=k+1时等式成立 B.n=k+2时等式成立
C.n=2k+2时等式成立 D.n=2（k+2）时等式成立
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷（解析版） 题型：选择题
某个命题与自然数n有关，若n=k（k∈N*）时命题成立，那么可推得当n=k+1时该命题也成立．现已知当n=5时，该命题不成立，那么可推得（ ）
A.当n=6时，该命题不成立 B.当n=6时，该命题成立
C.当n=4时，该命题不成立 D.当n=4时，该命题成立
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷（解析版） 题型：解答题
设a1，a2，…，an为正数，求证：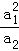
+
+…+
+
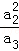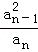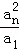≥a1+a2+…+an．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：填空题
（2014•黄浦区一模）设向量
=（a，b），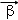
=（m，n），其中a，b，m，n∈R，由不等式|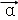
|
•|
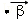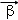|恒成立，可以证明（柯西）不等式（am+bn）2≤（a2+b2）（m2+n2）（当且仅当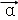
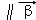，即an=bm时等号成立），己知x，y∈R+，若
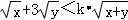恒成立，利用柯西不等式可求得实数k的取值范围是 ．
查看答案和解析>>
科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷（解析版） 题型：填空题
要证明“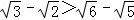
”可选择的方法有以下几种，其中最合理的是 ．（填序号）．①反证法，②分析法，③综合法．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
