
(2012•贵溪市模拟)设a、b、β为整数(β>0),若a和b被β除得的余数相同,则称a和b对β同余,记为a=b(modβ),已知a=1+C +C
+C •2+C
•2+C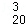 •22+…+C
•22+…+C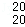 •219,b=a(mod10),则b的值可以是( )
•219,b=a(mod10),则b的值可以是( )
A.2010 B.2011 C.2012 D.2009
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-7 1.3黄金分割法-0.618法(解析版) 题型:填空题
(2012•怀化二模)用0.618法确定试点,经过4次试验后,存优范围缩小为原来的 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 4.1信息的加密与去密练习卷(解析版) 题型:填空题
为了确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文2a+b,2b+c,c+5d,2d,例如,明文1,2,3,4对应密文4,7,23,8,当接收方收到密文7,13,38,14时,则解密得到的明文是( )
A.27,64,108,24 B.64,27,108,24
C.1,3,5,7 D.1,5,3,7
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.4一次同余方程练习卷(解析版) 题型:选择题
(2012•贵溪市模拟)设a、b、β为整数(β>0),若a和b被β除得的余数相同,则称a和b对β同余,记为a=b(modβ),已知a=1+C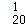 +C
+C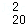 •2+C
•2+C •22+…+C
•22+…+C •219,b=a(mod10),则b的值可以是( )
•219,b=a(mod10),则b的值可以是( )
A.2010 B.2011 C.2012 D.2009
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 2.1同余练习卷(解析版) 题型:填空题
(2013•永州一模)若两整数a,b除以同一个整数m,所得余数相同,则称a,b对模m同余.即当a,b,m∈z时,若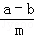 =k(k∈z,k≠0),则称a、b对模m同余,用符号a=b(modm)表示.
=k(k∈z,k≠0),则称a、b对模m同余,用符号a=b(modm)表示.
(1)若6=b(mod2)且0<b<6,则b的所有可能取值为 ;
(2)若a=10(modm)(a>10,m>1),满足条件的a由小到大依次记为a1,a2…an,…,当数列{an}前m﹣1项的和为60(m﹣1)时,则m= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
已知n为正偶数,用数学归纳法证明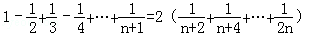 时,若已假设n=k(k≥2)为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立.
时,若已假设n=k(k≥2)为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立.
A.n=k+1 B.n=k+2 C.n=2k+2 D.n=2(k+2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com