练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．下列函数中，既是奇函数又在区间（0，+∞）上单调递增的函数是（　　）
    A．y=x+x-1B．y=x3+xC．y=2x+log2xD．$y={x^{\frac{1}{2}}}$

    分析 根据函数奇偶数和单调性的性质分别进行判断即可．

    解答 解：A．y=x+x-1是奇函数，在区间（0，+∞）不是单调函数，
    B．y=x3+x是奇函数，函数的导数y′=3x2+1＞0，则函数为增函数，满足条件．
    C．y=2x+log2x在（0，+∞）上为增函数，为非奇非偶函数．
    D.$y={x^{\frac{1}{2}}}$在[0，+∞）上为增函数，但函数为非奇非偶函数，
    故满足条件的是B，
    故选：B

    点评 本题主要考查函数奇偶性和单调性的判断，要求熟练掌握常见函数的奇偶性和单调性的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．定义[x]表示不超过x的最大整数（x∈R），如：[-1，3]=-2，[0，8]=0；定义{x}=x-[x]．
    （1）{$\frac{999}{1000}$}+{$\frac{99{9}^{2}}{1000}$}+{$\frac{99{9}^{3}}{1000}$}+{$\frac{99{9}^{4}}{1000}$}=2；
    （2）当n为奇数时，
    {$\frac{999}{1000}$}+{$\frac{99{9}^{2}}{1000}$}+{$\frac{99{9}^{3}}{1000}$}+…+{$\frac{99{9}^{n}}{1000}$}=$\frac{n-1}{2}+\frac{999}{1000}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线平行于直线l：y=2x+10，双曲线的一个焦点在直线l上，则双曲线的方程为（　　）
    A．$\frac{{3{x^2}}}{25}-\frac{{3{y^2}}}{100}=1$B．$\frac{{3{x^2}}}{100}-\frac{{3{y^2}}}{25}=1$
    C．$\frac{x^2}{20}-\frac{y^2}{5}=1$D．$\frac{x^2}{5}-\frac{y^2}{20}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．运行如图所示的程序框图，若输出的结果是36，则输入的n=（　　）
    A．6B．7C．8D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．甲、乙两同学的6次考试成绩分别为：
    甲998997859599
    乙899390899290
    （Ⅰ）画出甲、乙两同学6次考试成绩的茎叶图；
    （Ⅱ）计算甲、乙两同学考试成绩的方差，并对甲、乙两同学的考试成绩做出合理评价．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．过⊙O外一点P作⊙O的切线PA，切点为A，连OP与⊙O交于点C，过C作AP的垂线，垂足为D，若PA=8cm，PC=4cm，则PD的长为3.2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

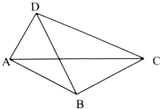
    12．四边形ABCD中，AB=BC，AD⊥DC，AC=1，∠ACD=θ，若$\overrightarrow{D{B}}•\overrightarrow{{A}C}=\frac{1}{3}$，则cos2θ等于（　　）
    A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．为了评价某个电视栏目的改革效果，在改革前后分别从居民点抽取了100位居民进行调查，经过计算K2≈0.99，根据这一数据分析，下列说法正确的是（　　）
    A．有99%的人认为该栏目优秀
    B．有99%的人认为该栏目是否优秀与改革有关系
    C．有99%的把握认为电视栏目是否优秀与改革有关系
    D．没有理由认为电视栏目是否优秀与改革有关系

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在△ABC中，角A，B，C的对边分别是a，b，c，若（2a+c）cosB+bcosC=0．
    （1）求角B的大小；
    （2）若a=3，△ABC的面积为$\frac{{3\sqrt{3}}}{2}$，求$\overrightarrow{AB}•\overrightarrow{BC}$的值．

    查看答案和解析>>

    同步练习册答案