
在直角坐标平面内,以坐标原点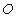 为极点,
为极点,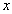 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线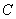 的极坐标方程是
的极坐标方程是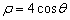 ,直线
,直线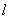 的参数方程是
的参数方程是 (
(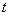 为参数).
为参数).
(Ⅰ)过极点作直线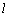 的垂线,垂足为点
的垂线,垂足为点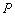 ,求点
,求点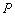 的极坐标;
的极坐标;
(Ⅱ)若点 分别为曲线
分别为曲线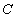 和直线
和直线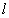 上的动点,求
上的动点,求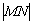 的最小值.
的最小值.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线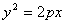
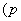 >
>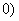 ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为 ( )
( )
A.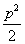 B.
B.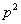 C.
C.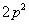 D.
D.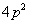
查看答案和解析>>
科目:高中数学 来源: 题型:
已知一个正四面体纸盒的俯视图如图所示,其中四边形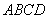 是边长为
是边长为 的正方形,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值为
的正方形,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值为
(A) (B)1
(B)1
(C)2 (D)

查看答案和解析>>
科目:高中数学 来源: 题型:
某花店每天以每枝10元的价格从农场购进若干支玫瑰花,并开始以每枝20元的价格出售,已知该花店的营业时间为8小时,若前7小时内所购进的玫瑰花没有售完,则花店对没卖出的玫瑰花以每枝5元的价格低价处理完毕(根据经验,1小时内完全能够把玫瑰花低价处理完毕,且处理完毕后,当天不再购进玫瑰花).该花店统计了100天内玫瑰花在每天的前7小时内的需求量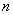 (单位:枝,
(单位:枝,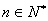 )(由于某种原因需求量频数表中的部分数据被污损而无法看清),制成如下表格(注:
)(由于某种原因需求量频数表中的部分数据被污损而无法看清),制成如下表格(注: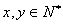 ;视频率为概率).
;视频率为概率).
| 前7小时内的需求量 | 14 | 15 | 16 | 17 |
| 频数 | 10 | 20 |
|
|
(Ⅰ)若花店一天购进16枝玫瑰花,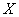 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求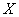 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)若花店每天购进16枝玫瑰花所获得的平均利润比每天购进17枝玫瑰花所获得的平均利润大,求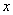 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
一支田径队有男女运动员98人,其中男运动员有56人.按男女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图是见证 魔术师“论证”64=65飞神奇.对这个乍看起来颇为神秘的现象,我们运用数学知识不难发现其中的谬误.另外,我们可以更换图中的数据,就能构造出许多更加直观与“令人信服”的“论证”.请你用数列知识归纳:(1)这些图中的数所构成的数列:________;(2)写出与这个魔术关联的一个数列递推关系式:________.
魔术师“论证”64=65飞神奇.对这个乍看起来颇为神秘的现象,我们运用数学知识不难发现其中的谬误.另外,我们可以更换图中的数据,就能构造出许多更加直观与“令人信服”的“论证”.请你用数列知识归纳:(1)这些图中的数所构成的数列:________;(2)写出与这个魔术关联的一个数列递推关系式:________.

查看答案和解析>>
科目:高中数学 来源: 题型:
定义集合M、N的新运算如下:Mx N={x|x∈M或x∈N,但x∉M∩N},若集合M={0,2,4,6,8,10},N={0,3,6,9,12,15},则(Mx N)xM等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com