练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    　设a、b、c均为大于1的正数，且ab＝10，求证：logac＋logbc≥4lgc.


    证明：(分析法)由于a>1，b>1，c>1，故要证明logac＋logbc≥4lgc，只要证明≥4lgc，即≥4，因为ab＝10，故lga＋lgb＝1.只要证明≥4，由于a>1，b>1，故lga>0，lgb>0，所以0<lgalgb≤＝2＝，即≥4成立．所以原不等式成立．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    若点O和点F分别为椭圆＝1的中心和左焦点，点P为椭圆上的任意一点，则的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知△ABC外接圆半径R＝，且∠ABC＝120°，BC＝10，边BC在x轴上且y轴垂直平分BC边，则过点A且以B、C为焦点的双曲线方程为______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面几何里可以得出正确结论：“正三角形的内切圆半径等于这正三角形的高的”．拓展到空间，类比平面几何的上述结论，则正四面体的内切球半径等于这个正四面体的高的________ .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明命题“如果a>b，那么”时，假设的内容应为______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a、b、c∈(0，＋∞)且a＜c，b＜c，＋＝1，若以a、b、c为三边构造三角形，则c的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若f(n)＝1＋＋＋…＋ (n∈N)，则n＝1时，f(n)＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明“12＋22＋32＋…＋n2＝n(n＋1)(2n＋1)(n∈N*)”，当n＝k＋1时，应在n＝k时的等式左边添加的项是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角坐标平面内，以坐标原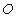点为极点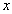，轴的正半轴为极轴建立极坐标系，曲线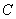的极坐标方程是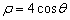，直线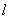的参数方程是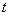（为参数）.

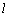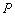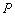       （Ⅰ）过极点作直线的垂线，垂足为点，求点的极坐标；

       （Ⅱ）若点分别为曲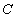线和直线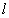上的动点，求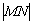的最小值.

    查看答案和解析>>

    同步练习册答案