
| A. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(-1,2) | B. | $\overrightarrow{{e}_{1}}$=(-1,3),$\overrightarrow{{e}_{2}}$=(2,-6) | ||
| C. | $\overrightarrow{{e}_{1}}$=(-1.2),$\overrightarrow{{e}_{2}}$=(3,-1) | D. | $\overrightarrow{{e}_{1}}$=(-$\frac{1}{2}$,1),$\overrightarrow{{e}_{2}}$=(1,-2) |
分析 根据条件知$\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}$可表示向量$\overrightarrow{a}$,从而需满足$\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}$不共线,从而找出不共线的$\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}$即可.
解答 解:$\overrightarrow{a}$$≠\overrightarrow{0}$,$\overrightarrow{{e}_{1}}和\overrightarrow{{e}_{2}}$可以表示$\overrightarrow{a}$,∴$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$不共线;
A.$\overrightarrow{{e}_{1}}=0•\overrightarrow{{e}_{2}}$,∴$\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}$共线;
B.$\overrightarrow{{e}_{2}}=-2\overrightarrow{{e}_{1}}$,∴$\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}$共线;
C.-1×(-1)-2×3≠0,∴$\overrightarrow{{e}_{1}},\overrightarrow{{e}_{2}}$不共线,∴该选项正确;
D.$\overrightarrow{{e}_{2}}=-2\overrightarrow{{e}_{1}}$,∴$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$共线.
故选:C.
点评 考查平面向量基本定理,以及共面向量基本定理,共线向量的坐标关系.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:填空题
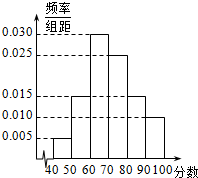 某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.
某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (0,2) | C. | (-1,0) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4,5,6} | B. | {3} | C. | {3,4,5,6} | D. | {1,2,3,4,5,6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com