
【题目】设函数![]() 在
在![]() 上有定义,实数
上有定义,实数![]() 和
和![]() 满足
满足![]() ,若
,若![]() 在区间
在区间![]() 上不存在最小值,则称
上不存在最小值,则称![]() 在
在![]() 上具有性质
上具有性质![]() .
.
(1)当![]() ,且
,且![]() 在区间
在区间![]() 上具有性质
上具有性质![]() 时,求常数
时,求常数![]() 的取值范围;
的取值范围;
(2)已知![]() (
(![]() ),且当
),且当![]() 时,
时,![]() ,判别
,判别![]() 在区间
在区间![]() 上是否具有性质
上是否具有性质![]() ,试说明理由.
,试说明理由.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 以及曲线
以及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,函数F(x)=f(x)﹣b有四个不同的零点x1,x2,x3,x4,且满足:x1<x2<x3<x4,则
,函数F(x)=f(x)﹣b有四个不同的零点x1,x2,x3,x4,且满足:x1<x2<x3<x4,则![]() 的取值范围是( )
的取值范围是( )
A.[![]() ,+∞)B.(3,
,+∞)B.(3,![]() ]C.[3,+∞)D.
]C.[3,+∞)D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )

A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 的参数方程为
的参数方程为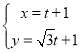 ,(
,(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ),过点
),过点![]() (
(![]() )的直线
)的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若![]() ,求证:
,求证:![]() 是定值(
是定值(![]() 是坐标原点);
是坐标原点);
(2)若![]() (
(![]() 是确定的常数),求证:直线
是确定的常数),求证:直线![]() 过定点,并求出此定点坐标;
过定点,并求出此定点坐标;
(3)若![]() 的斜率为1,且
的斜率为1,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元,为了增加企业竞争力,决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业,调整后这
)名员工从事第三产业,调整后这![]() 名员工他们平均每人创造利润为
名员工他们平均每人创造利润为![]() 万元,剩下的员工平均每人每年创造的利润可以提高
万元,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整多少名员工从事第三产业?
(2)设![]() ,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,求
,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com