
分析 由α+β=$\frac{π}{12}$,结合两角和的正切可得1-tanαtanβ=$(2-\sqrt{3})(tanα+tanβ)$,代入$\frac{1-tanα-tanβ-tanα•tanβ}{1+tanα+tanβ-tanα•tanβ}$后整理得答案.
解答 解:由α+β=$\frac{π}{12}$,得
$tan(α+β)=tan(\frac{π}{3}-\frac{π}{4})=\frac{tan\frac{π}{3}-tan\frac{π}{4}}{1+tan\frac{π}{3}tan\frac{π}{4}}$=$\frac{\sqrt{3}-1}{\sqrt{3}+1}$,
即$\frac{tanα+tanβ}{1-tanα•tanβ}=\frac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}$,
∴1-tanαtanβ=$(2-\sqrt{3})(tanα+tanβ)$,
∴$\frac{1-tanα-tanβ-tanα•tanβ}{1+tanα+tanβ-tanα•tanβ}$=$\frac{(2-\sqrt{3})(tanα+tanβ)-(tanα+tanβ)}{(2-\sqrt{3})(tanα+tanβ)+(tanα+tanβ)}$
=$\frac{1-\sqrt{3}}{3+\sqrt{3}}=\frac{(1-\sqrt{3})(3-\sqrt{3})}{(3+\sqrt{3})(3-\sqrt{3})}=\frac{6-4\sqrt{3}}{6}=\frac{3-2\sqrt{3}}{3}$.
点评 本题考查两角和与差的正切函数,考查了计算能力,是中档题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [--4,$\frac{\sqrt{3}+1}{2}$] | B. | [-$\frac{\sqrt{3}+1}{2}$,$\frac{1-\sqrt{5}}{2}$] | C. | [-$\frac{\sqrt{3}+1}{2}$,$\frac{1+\sqrt{5}}{2}$] | D. | [-4,$\frac{1+\sqrt{5}}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
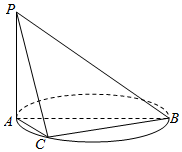 如图,AB时圆O的直径,PA垂直圆所在的平面,C是圆上异于A、B的动点,PA=AB,∠ABC大小为θ,点D、E分别在棱PB,PC上.
如图,AB时圆O的直径,PA垂直圆所在的平面,C是圆上异于A、B的动点,PA=AB,∠ABC大小为θ,点D、E分别在棱PB,PC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com