
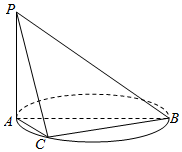
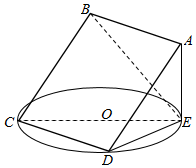
 如图,AB时圆O的直径,PA垂直圆所在的平面,C是圆上异于A、B的动点,PA=AB,∠ABC大小为θ,点D、E分别在棱PB,PC上.
如图,AB时圆O的直径,PA垂直圆所在的平面,C是圆上异于A、B的动点,PA=AB,∠ABC大小为θ,点D、E分别在棱PB,PC上.分析 (1)根据线面垂直的判定定理即可证明BC⊥平面PAC;
(2)根据直二面角的定义,进行判断即可;
(3)根据线面垂直的定义和性质,建立三角函数关系,利用基本不等式的性质进行求解即可.
解答 解:(1)∵PA垂直圆所在的平面,∴PA⊥BC,
∵AB时圆O的直径,
∴BC⊥AC,
∵AC∩PA=A,
∴BC⊥平面PAC;
(2)存在点E,当DE∥BC时,使得二面角A-DE-P为直二面角
若DE∥BC,又由(1)知,BC⊥平面PAC,
∴DE⊥平面PAC.
又∵AE?平面PAC,PE?平面PAC,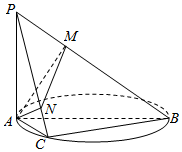
∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角A-DE-P的平面角.
∵PA⊥底面ABC,∴PA⊥AC,
∴∠PAC=90°,∴在棱PC上存在一点E,使得AE⊥PC.
这时,∠AEP=90°,
故存在点E使得二面角A-DE-P是直二面角.
(3)不妨设PB=2a,则PA=PB=$\sqrt{2}$a,
则由$\left.\begin{array}{l}{PB⊥面AMN}\\{AM?面AMN}\end{array}\right\}$⇒AM⊥PB,
在△PAB中,AP=PB,则AM=MB=a,
又PB⊥面AMN,AN?面AMN,∴AN⊥PB,
BC⊥面PAC,AN?面AMN,∴AN⊥BC,
∵BC∩PB=B,
∴AN⊥面PAC,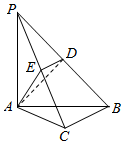
∵MN?面AMN,
∴AN⊥MN,
则△AMN直角三角形,
又斜边AM=a为定长,AM2=AN2+MN2≥2AN•MN,
于是S△AMN=$\frac{1}{2}$AN•MN≤$\frac{A{N}^{2}+M{N}^{2}}{4}$=$\frac{{a}^{2}}{4}$,
∴当△AMN为等腰直角三角形时,面积最大,
此时AN=MN=$\frac{\sqrt{2}a}{2}$,在直角三角形PAC中,得PA=$\sqrt{2}$a,AN=$\frac{\sqrt{2}a}{2}$,AC=$\frac{\sqrt{6}a}{3}$,
直角三角形PAC中,得AB=$\sqrt{2}$a,AC=$\frac{\sqrt{6}a}{3}$,
∴sinθ=$\frac{AC}{AB}$=$\frac{\sqrt{3}}{3}$,
即sinθ=$\frac{\sqrt{3}}{3}$时,△AMN的面积S有最大值.
点评 本题主要考查直线和平面垂直的判断,以及线面垂直以及二面角的应用,利用定义法结合相应的判定定理和性质定理是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E、F、H分别为AD、CD、DD1的中点,EF与BD交于点G.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E、F、H分别为AD、CD、DD1的中点,EF与BD交于点G.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
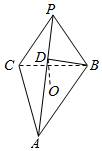 三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心.
三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径为9.
如图所示,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C,D的点,AE=3,圆O的直径为9.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点P是⊙O圆周上异于A,B的一点,AD⊥⊙O所在的平面PAB,四边形ABCD是边长为2的正方形,连结PA,PB,PC,PD.
如图,AB是⊙O的直径,点P是⊙O圆周上异于A,B的一点,AD⊥⊙O所在的平面PAB,四边形ABCD是边长为2的正方形,连结PA,PB,PC,PD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若x≠a且x≠b,则x2-(a+b)x+ab≠0”的否命题是“若x=a或x=b,则x2-(a+b)x+ab=0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | 命题“?x0∈(0,+∞)lnx0=x0-1”的否定是“?x∈(0,+∞),lnx≠x-1 | |
| D. | “x>2”是“$\frac{1}{x}$<$\frac{1}{2}$”的充分不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com