
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
分析 设小圆锥的半径为r,大圆锥的半径为R;母线长分别为l,L;高分别为h,H.由于用平行于圆锥底面的截面去截圆锥,可得$\frac{r}{R}=\frac{l}{L}=\frac{h}{H}$.利用圆锥侧面积计算公式即可得出.
解答 解:设小圆锥的半径为r,大圆锥的半径为R;
母线长分别为l,L;高分别为h,H.
∵用平行于圆锥底面的截面去截圆锥,
则$\frac{r}{R}=\frac{l}{L}=\frac{h}{H}$.
由小圆锥的侧面积与原来大圆锥的侧面积的比是$\frac{1}{2}$,
则$\frac{\frac{1}{2}•2πr•l}{\frac{1}{2}•2πR•L}$=$\frac{1}{2}$,∴$\frac{{h}^{2}}{{H}^{2}}=\frac{1}{2}$.
∴$\frac{h}{H}$=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题考查了圆锥侧面积计算公式、相似三角形的性质,考查了推理能力与计算能力,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
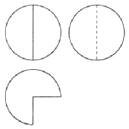 如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )
如图,某几何体的三视图由半径相同的圆和扇形构成,若府视图中扇形的面积为3π,則该几何体的体积等于( )| A. | 8π | B. | $\frac{16π}{3}$ | C. | 4π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$个 | B. | $\frac{π}{3}$个 | C. | $\frac{π}{4}$个 | D. | $\frac{π}{12}$个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ | $\frac{9π}{2}$ |
| Asin(ωx+φ) | 0 | 3 | 0 | -3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com