
设a∈R,函数f(x)=x·|x-a|+2x.
(1) 若a=2,求函数f(x)在区间[0,3]上的最大值;
(2) 若a>2,写出函数f(x)的单调区间(不必证明);
(3) 若存在a∈[-2,4],使得关于x的方程f(x)=t·f(a)有3个不相等的实数解,求实数t的取值范围.
(1) 当a=2,x∈[0,3]时,f(x)=x·|x-2|+2x=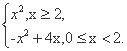
作函数图象(图象略),可知函数f(x)在区间[0,3]上是单调增函数,所以f(x)的最大值为f(3)=9.
(2) f(x)=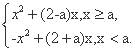
①当x≥a时,f(x)=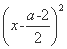 -
- ,
,
因为a>2,所以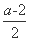 <a,
<a,
所以函数f(x)在[a,+∞)上单调递增.
②当x<a时,f(x)=- +
+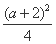 ,
,
因为a>2,所以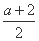 <a,所以函数f(x)在
<a,所以函数f(x)在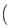 -∞,
-∞,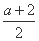
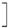 上单调递增,在
上单调递增,在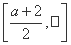 上单调递减.
上单调递减.
综上,函数f(x)的单调增区间是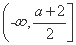 和[a,+∞),单调减区间是
和[a,+∞),单调减区间是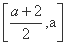 .
.
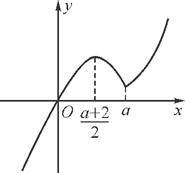
(第11题)
(3) ①当-2≤a≤2时,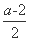 ≤0,
≤0,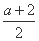 ≥0,所以函数f(x)在(-∞,+∞)上是增函数,
≥0,所以函数f(x)在(-∞,+∞)上是增函数,
关于x的方程f(x)=t·f(a)不可能有三个不相等的实数解.
②当2<a≤4时,由(2)知函数f(x)在区间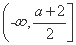 和[a,+∞)上分别是增函数,在区间
和[a,+∞)上分别是增函数,在区间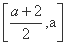 上是减函数,所以当且仅当2a<t·f(a)<
上是减函数,所以当且仅当2a<t·f(a)<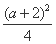 时,方程f(x)=t·f(a)有三个不相等的实数解,
时,方程f(x)=t·f(a)有三个不相等的实数解,
即1<t< =
=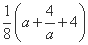 .
.
令g(a)=a+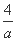 ,g (a)在a∈(2,4]时是增函数,故g(a)max=5,
,g (a)在a∈(2,4]时是增函数,故g(a)max=5,
所以,实数t的取值范围是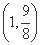 .
.


科目:高中数学 来源: 题型:
是否存在这样的实数a,使函数f(x)=x2+(3a-2)x+a-1在区间[-1,3]上与x轴有且只有一个交点.若存在,求出a的范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
5.据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图像如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
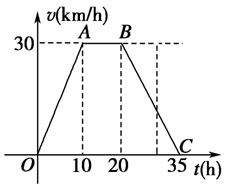
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com