是否存在这样的实数a，使函数f(x)＝x2＋(3a－2)x＋a－1在区间[－1,3]上与x轴有且只有一个交点．若存在，求出a的范围；若不存在，说明理由．
∵Δ＝(3a－2)2－4(a－1)>0，
∴若存在实数a满足条件，则只需f(－1)·f(3)≤0即可．
f(－1)·f(3)＝(1－3a＋2＋a－1)·(9＋9a－6＋a－1)
＝4(1－a)(5a＋1)≤0.
所以a≤－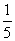
或a≥1.检验：①当f(－1)＝0时，a＝1.
所以f(x)＝x2＋x.令f(x)＝0，
即x2＋x＝0，得x＝0或x＝－1.
方程在[－1,3]上有两根，不合题意，故a≠1.
②当f(3)＝0时，a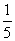＝－，此时f(x)＝x2－
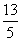x－
，
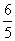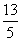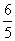令f(x)＝0，即x2－x－＝0，
解之得x＝－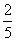
或x＝3.
方程在[－1,3]上有两根，不合题意，故a≠－.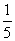
综上所述，a<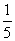－或a>1.
名校课堂系列答案科目：高中数学 来源： 题型：
已知定义域为R的函数f(x)为奇函数，且满足f(x＋2)＝－f(x)，当x∈[0,1]时，f(x)＝2x－1.
(1)求f(x)在[－1,0)上的解析式；
(2)求f(log
24)的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知f(x)＝(x－a)(x－b)－2(a<b)，并且α、β是方程f(x)＝0的两个根(α<β)，则实数a、b、α、β的大小关系可能是( )
A．α<a<b<β B．a<α<β<b
C．a<α<b<β D．α<a<β<b
查看答案和解析>>
科目：高中数学 来源： 题型：
系数丛书2014年的销量比2012的销量增长44%，若每年的平均增长率相同(设为x)，则以下结论正确的是( )
A．x>22%
B．x<22%
C．x＝22%
D．x的大小由第一年的销量确定
查看答案和解析>>
科目：高中数学 来源： 题型：
某商人将进货单价为8元的某种商品按10元一个销售时，每天可卖出100个，现在他采用提高售价，减少进货量的办法增加利润，已知这种商品销售单价每涨1元，销售量就减少10个，问他将售价每个定为多少元时，才能使每天所赚的利润最大？并求出最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
设a∈R,函数f(x)=x·|x-a|+2x.
(1) 若a=2,求函数f(x)在区间[0,3]上的最大值;
(2) 若a>2,写出函数f(x)的单调区间(不必证明);
(3) 若存在a∈[-2,4],使得关于x的方程f(x)=t·f(a)有3个不相等的实数解,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，0) B．(－1，－