练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)＝mx2－2x＋1有且仅有一个正实数的零点，则实数m的取值范围是________．


    　(－∞，0]∪{1}

    [解析]　当m＝0时，x＝为函数的零点；

    当m≠0时，若Δ＝0，即m＝1时，x＝1是函数唯一的零点，

    若Δ≠0，显然函数x＝0不是函数的零点，这样函数有且仅有一个正实数零点等价于方程mx2－2x＋1＝0有一个正根和一个负根，即mf(0)<0，即m<0.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    函数f(x)＝ax＋loga(x＋1)在[0,1]上的最大值和最小值之和为a，则a的值为(　　)

    A.                                                             B.

    C．2                                                             D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数y＝lg(3－4x＋x2)的定义域为M.当x∈M时，求f(x)＝2x＋2－3×4x的最值及相应的x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数y＝f(x)(x∈R)满足f(x＋2)＝f(x)且x∈[－1,1]时，f(x)＝1－x2，函数g(x)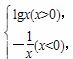＝则函数h(x)＝f(x)－g(x)在区间[－5,5]内的零点的个数为(　　)

    A．5                                                             B．7

    C．8                                                             D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)＝ax＋b(a≠0)有一个零点是2，那么函数g(x)＝bx2－ax的零点是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    是否存在这样的实数a，使函数f(x)＝x2＋(3a－2)x＋a－1在区间[－1,3]上与x轴有且只有一个交点．若存在，求出a的范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某汽车运输公司，购买了一批豪华大客车投入营运，据市场分析每辆客车营运的总利润y(单位：10万元)与营运年数x(x∈N)为二次函数关系(如图所示)，则每辆客车营运多少年，其营运的平均利润最大(　　)

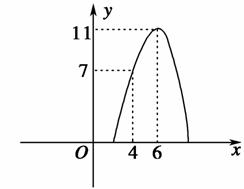
    A．3                                                             B．4

    C．5                                                             D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=x,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    化简＝______(k∈Z)．

    查看答案和解析>>

    同步练习册答案