【题目】设函数
.
（1）若
，求
的单调区间；
（2）若
，讨论
当
时的零点的个数.
【答案】（1）见解析（2）见解析
【解析】试题分析：（1）由解析式求出定义域和
，化简后对
进行分类讨论，根据导数与函数单调性的关系，分别求出函数的增区间、减区间；（2）由（1）求函数的最小值，由条件列出不等式求出
的范围，对
进行分类讨论，并分别判断在区间
上的单调性，求出
和
判断出符号，即可得结论.
试题解析：（1）
，
①
， 
， 
， 
增.
②
， 
，有
的增区间
.
，有
的减区间为
.
（2）①
时，有
，在
单调递减，
， 
，在
上有一个零点.
②
时，有
，在
单调递减，
，在
上没有零点.
③
时，有
，在
单调递减，在
单调递增，
，在
上没有零点.
④
时， 
，在
上单调递增，
在
上没有零点.
综上所述①
在
上有一个零点，
②
，在
上没有零点.
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】已知直线
的方程为
，点
是抛物线
上到直线
距离最小的点，点
是抛物线上异于点
的点，直线
与直线
交于点
，过点
与
轴平行的直线与抛物线
交于点
.
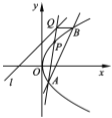
（Ⅰ）求点
的坐标；
（Ⅱ）证明直线
恒过定点，并求这个定点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为
（1）求频率分布图中
的值，并估计该企业的职工对该部门评分不低于80的概率；
（2）从评分在
的受访职工中，随机抽取2人，求此2人评分都在
的概率．．
查看答案和解析>>
科目：高中数学 来源： 题型：
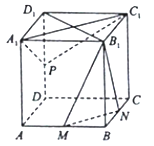
【题目】如图，正方体
中，
分别为
的中点.
（1）求证:平面
⊥平面
；
（2）当点
在
上运动时，是否都有
平面
，证明你的结论；
（3）若是的中点，求
与
所成的角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解学生身高情况，某校以
的比例对全校1000名学生按性别进行分层抽样调查，已知男女比例为
，测得男生身高情况的频率分布直方图（如图所示）：
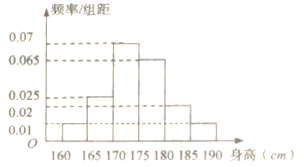
（1）计算所抽取的男生人数，并估计男生身高的中位数（保留两位小数）；
（2）从样本中身高在
之间的男生中任选2人，求至少有1人身高在
之间的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中心在坐标原点，焦点在
轴上的椭圆，离心率为
且过点
，过定点
的动直线与该椭圆相交于
、
两点.
（1）若线段
中点的横坐标是
，求直线
的方程；
（2）在
轴上是否存在点
，使
为常数？若存在，求出点
的坐标；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
