
【题目】已知函数![]()
(1)求![]() 的最小正周期和最大值;
的最小正周期和最大值;
(2)讨论![]() 的单调性。
的单调性。
【答案】(1) 最小正周期为π,最大值为![]()
(2) 在![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
【解析】试题分析:
(1)整理函数的解析式为![]() ,据此可得最小正周期为π,最大值为
,据此可得最小正周期为π,最大值为![]()
(2)利用(1)中函数的解析式可得函数在![]() 上单调递增;在
上单调递增;在![]() 上单调递减
上单调递减
试题解析:
(1)f(x)=cosxsinx-![]() cos2x
cos2x
=cosxsinx-![]() (1+cos2x)
(1+cos2x)
=![]() sin2x-
sin2x-![]() cos2x-
cos2x-![]()
=sin(2x-![]() )-
)-![]() ,
,
因此f(x)的最小正周期为π,最大值为 1-![]()
(2)由正弦曲线的单调性可知,由-![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2 kπ.可得单调增区间
+2 kπ.可得单调增区间
-![]() +kπ ≤x≤
+kπ ≤x≤ ![]() +kπ
+kπ
由 ![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2 kπ,可得单调减区间
+2 kπ,可得单调减区间
![]() +kπ ≤x≤
+kπ ≤x≤ ![]() +kπ
+kπ
所以f(x)在[-![]() +2kπ,
+2kπ, ![]() +2kπ]上单调递增;在[
+2kπ]上单调递增;在[![]() +kπ,
+kπ, ![]() +kπ]上单调递减.
+kπ]上单调递减.


科目:高中数学 来源: 题型:
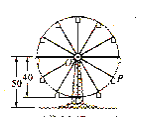
【题目】如图所示,摩天轮的半径为![]() 米,点
米,点![]() 距地面高度为
距地面高度为![]() 米,摩天轮做匀速运动,每
米,摩天轮做匀速运动,每![]() 分钟转一圈,以点
分钟转一圈,以点![]() 为原点,过点
为原点,过点![]() 且平行与地平线的直线为
且平行与地平线的直线为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,设点
,设点![]() 的起始位置在最低点(且在最低点开始时),设在时刻
的起始位置在最低点(且在最低点开始时),设在时刻![]() (分钟)时点
(分钟)时点![]() 距地面的高度
距地面的高度![]() (米),则
(米),则![]() 与
与![]() 的函数关系式
的函数关系式
![]()
![]() __________.在摩天轮旋转一周内,点
__________.在摩天轮旋转一周内,点![]() 到地面的距离不小于
到地面的距离不小于![]() 米的时间长度为 __________(分钟)
米的时间长度为 __________(分钟)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位射击运动员,在某天训练中已各射击10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
(Ⅰ)通过计算估计,甲、乙二人的射击成绩谁更稳;
(Ⅱ)若规定命中8环及以上环数为优秀,以频率作为概率,请依据上述数据估计,求甲在第11至第13次射击中获得优秀的次数![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:
方案一:每户每月收取管理费2元,月用电量不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取;
方案二:不收管理费,每度0.58元.
(1)求方案一![]() 收费(元)与用电量
收费(元)与用电量![]() (度)间的函数关系;
(度)间的函数关系;
(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?
(3)老王家该月用电量在什么范围内,选择方案一比选择方案二更好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 在
在![]() 的最小值;
的最小值;
(2)若函数![]() 与
与![]() 的图象恰有一个公共点,求实数
的图象恰有一个公共点,求实数![]() 的值;
的值;
(3)若函数![]() 有两个不同的极值点
有两个不同的极值点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com