
【题目】已知四棱柱![]() 的底面是边长为
的底面是边长为![]() 的菱形,且
的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,设
,设![]() 为
为![]() 的中点
的中点
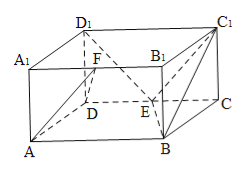
(1)求证:![]() 平面
平面![]()
(2)点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成锐角的余弦值.
所成锐角的余弦值.
【答案】(1)证明略;(2)![]()
【解析】
试题分析:(1)由已知该四棱柱为直四棱柱,且![]() 为等边三角形,
为等边三角形,![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() ,在
,在![]() 中的三边长分别为
中的三边长分别为![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,则由
,则由![]() 为等边三角形,知
为等边三角形,知![]() ,从而
,从而![]() ,以
,以![]() 为坐标轴,建立空间直角的坐标系,求得平面
为坐标轴,建立空间直角的坐标系,求得平面![]() 和平面
和平面![]() 的法向量,即可求得平面
的法向量,即可求得平面![]() 和平面
和平面![]() 所成锐角的余弦值.
所成锐角的余弦值.
试题解析:(1)证明:由已知该四棱柱为直四棱柱,且![]() 为等边三角形,
为等边三角形,![]()
所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,故
,故![]()
因为![]() 的三边长分别为
的三边长分别为![]() ,故
,故![]() 为等腰直角三角形
为等腰直角三角形
所以![]() ,结合
,结合![]() 知:
知:![]() 平面
平面![]()
(2)解:取![]() 中点
中点![]() ,则由
,则由![]() 为等边三角形
为等边三角形
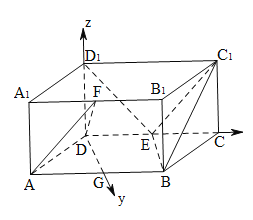
知![]() ,从而
,从而![]()
以![]() 为坐标轴,建立如图所示的坐标系
为坐标轴,建立如图所示的坐标系
此时![]() ,
,
![]() ,设
,设![]()
由上面的讨论知平面![]() 的法向量为
的法向量为![]()
由于![]() 平面
平面![]() ,故
,故![]() 平面
平面![]()
![]()
故![]() ,故
,故![]()
设平面![]() 的法向量为
的法向量为![]() ,
,![]()
由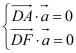 知
知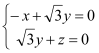 ,取
,取![]() ,故
,故![]()
设平面![]() 和平面
和平面![]() 所成锐角为
所成锐角为![]() ,则
,则
即平面![]() 和平面
和平面![]() 所成锐角的余弦值为
所成锐角的余弦值为![]()


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图“月亮图”是由曲线![]() 与
与![]() 构成,曲线
构成,曲线![]() 是以原点
是以原点![]() 为中点,
为中点, ![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以
是以![]() 为顶点,
为顶点, ![]() 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, ![]() 是两条曲线的一个交点.
是两条曲线的一个交点.
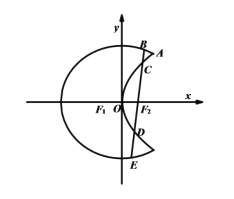
(Ⅰ)求曲线![]() 和
和![]() 的方程;
的方程;
(Ⅱ)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于
依次交于![]() 四点,若
四点,若![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,问:
的中点,问: ![]() 是否为定值?若是求出该定值;若不是说明理由.
是否为定值?若是求出该定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
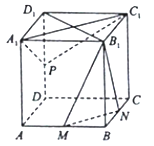
【题目】如图,正方体![]() 中,
中,![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)当点![]() 在
在![]() 上运动时,是否都有
上运动时,是否都有![]() 平面
平面![]() ,证明你的结论;
,证明你的结论;
(3)若![]() 是
是![]() 的中点,求
的中点,求![]() 与
与![]() 所成的角的余弦值.
所成的角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率![]() ,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,下图是根据刘徽的“割圆术”思想设计的一个程序框图,若运行该程序,则输出的
,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,下图是根据刘徽的“割圆术”思想设计的一个程序框图,若运行该程序,则输出的![]() 的值为( )(参考数据:
的值为( )(参考数据: ![]() ,
, ![]() ,
, ![]() )
)
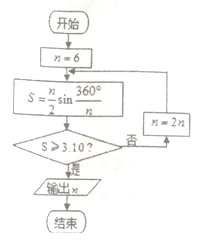
A. 24 B. 30 C. 36 D. 48
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有13名医生,其中女医生6人,现从中抽调5名医生组成医疗小组前往灾区,若医疗小组至少有2名男医生,同时至多有3名女医生,设不同的选派方法种数为N,则下列等式:
①C135﹣C71C64;②C72C63+C73C62+C74C61+C75;
③C135﹣C71C64﹣C65; ④C72C113;
其中能成为N的算式是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销量价格P(元)的关系如图所示;③每月需各种开支2 000元.
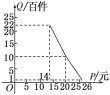
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com