
【题目】甲、乙两位射击运动员,在某天训练中已各射击10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
(Ⅰ)通过计算估计,甲、乙二人的射击成绩谁更稳;
(Ⅱ)若规定命中8环及以上环数为优秀,以频率作为概率,请依据上述数据估计,求甲在第11至第13次射击中获得优秀的次数![]() 的分布列和期望.
的分布列和期望.
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润![]() 取到最大值?(结果保留两位小数)
取到最大值?(结果保留两位小数)
参考公式: 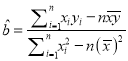 ,
, ![]()
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
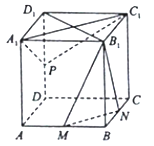
【题目】如图,正方体![]() 中,
中,![]() 分别为
分别为![]() 的中点.
的中点.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)当点![]() 在
在![]() 上运动时,是否都有
上运动时,是否都有![]() 平面
平面![]() ,证明你的结论;
,证明你的结论;
(3)若![]() 是
是![]() 的中点,求
的中点,求![]() 与
与![]() 所成的角的余弦值.
所成的角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):
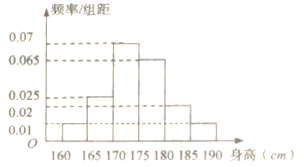
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有13名医生,其中女医生6人,现从中抽调5名医生组成医疗小组前往灾区,若医疗小组至少有2名男医生,同时至多有3名女医生,设不同的选派方法种数为N,则下列等式:
①C135﹣C71C64;②C72C63+C73C62+C74C61+C75;
③C135﹣C71C64﹣C65; ④C72C113;
其中能成为N的算式是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,得曲线
轴的正半轴为极轴建立极坐标系,得曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() .
.
(1)化曲线![]() 的参数方程为普通方程,化曲线
的参数方程为普通方程,化曲线![]() 的极坐标方程为直角坐标方程;
的极坐标方程为直角坐标方程;
(2)直线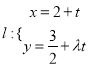 (
(![]() 为参数)过曲线
为参数)过曲线![]() 与
与![]() 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线![]() 平行且与曲线
平行且与曲线![]() 相切的直线方程.
相切的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com