Question

【题目】为了解学生身高情况，某校以的比例对全校1000名学生按性别进行分层抽样调查，已知男女比例为，测得男生身高情况的频率分布直方图（如图所示）：

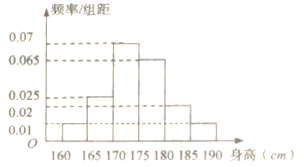
（1）计算所抽取的男生人数，并估计男生身高的中位数（保留两位小数）；

（2）从样本中身高在之间的男生中任选2人，求至少有1人身高在之间的概率．

Answer 1

【答案】(1)174.64cm(2).

【解析】试题分析：

(1)由题意结合中位数的求法可得男生身高的中位数是174.64cm；

(2)列出所有可能的事件，结合古典概型公式可得至少有1人身高在之间的概率是.

试题解析：

(1)由题意得，所抽取的男生人数为：

1000×8%×=40人

依据样本频率分布直方图：0.01×5+0.025×5+x=0.5 得x=0.325 ，而身高170~175之间的频率为0.35，所以中位数为170+5×≈174.64cm

(2)样本中身高在180～185 cm之间的男生有4人，设其编号为①，②，③，④，样本中身高在185～190 cm之间的男生有2人，设其编号为⑤，⑥，从上述6人中任取2人的共有：

（①，②）（①，③）（①，④）（①，⑤）（①，⑥）

（②，③）（②，④）（②，⑤）（②，⑥）

（③，④）（③，⑤）（③，⑥）

（④，⑤）（④，⑥）

（⑤，⑥）

故从样本中身高在180～190 cm之间的男生中任选2人的所有可能结果数为15，至少有1人身高在185～190 cm之间的可能结果数为9，因此，所求概率P2＝＝.